
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Номер 121 Дорофеев, Суворова — Подробные Ответы
Для функций у = f(x) и у = g(x) найдите множество значений аргумента, на котором обе функции отрицательны; одна из них отрицательна, а другая положительна; обе положительны. Проиллюстрируйте своё решение с помощью графиков.
а) ,
б) ,
а) Функции и :
1)Обе функции отрицательны:
2)Функция
3)Функция
Таких значений аргумента не существует;
4)Обе функции положительны:
7)График функций:
б) Функции
1)Обе функции отрицательны:
2)Функция
3)Функция
4)Обе функции положительны:
Таких значений аргумента не существует;
)График функций:
а) Функции
Обе функции отрицательны:
Рассмотрим систему неравенств:
Решим первое неравенство
Прибавим 1 к обеим частям:
Разделим обе части на 2:
Решим второе неравенство
Объединяем оба неравенства:
Функция
Рассмотрим систему неравенств:
Решим первое неравенство
Прибавим 1 к обеим частям:
Разделим обе части на 2:
Решим второе неравенство
Объединяем оба неравенства:
Функция
Рассмотрим систему неравенств:
Решим первое неравенство
Прибавим 1 к обеим частям:
Разделим обе части на 2:
Решим второе неравенство
Так как
Обе функции положительны:
Рассмотрим систему неравенств:
Решим первое неравенство
Прибавим 1 к обеим частям:
Разделим обе части на 2:
Решим второе неравенство
Объединяем оба неравенства:
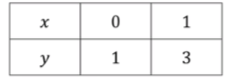
Для
Для
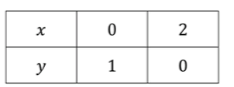
Таблица значений:
Для
Для
Таблица значений:
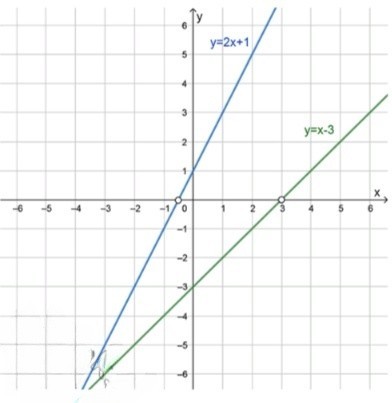
График функций:
б) Функции
Обе функции отрицательны:
Рассмотрим систему неравенств:
Решим первое неравенство
Вычитаем 1 из обеих частей:
Умножаем обе части на -2 (при этом знак неравенства меняется):
Решим второе неравенство
Прибавим 2 к обеим частям:
Умножаем обе части на 2:
Объединяем оба неравенства:
Функция
Рассмотрим систему неравенств:
Решим первое неравенство
Вычитаем 1 из обеих частей:
Умножаем обе части на -2 (при этом знак неравенства меняется):
Решим второе неравенство
Прибавим 2 к обеим частям:
Умножаем обе части на 2:
Объединяем оба неравенства:
Функция
Рассмотрим систему неравенств:
Решим первое неравенство
Вычитаем 1 из обеих частей:
Умножаем обе части на -2 (при этом знак неравенства меняется):
Решим второе неравенство
Прибавим 2 к обеим частям:
Умножаем обе части на 2:
Объединяем оба неравенства:
Обе функции положительны:
Рассмотрим систему неравенств:
Решим первое неравенство
Вычитаем 1 из обеих частей:
Умножаем обе части на -2 (при этом знак неравенства меняется):
Решим второе неравенство
Прибавим 2 к обеим частям:
Умножаем обе части на 2:
Так как нет таких значений
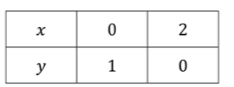
Для
Для
Таблица значений:
Для
Для
Таблица значений:
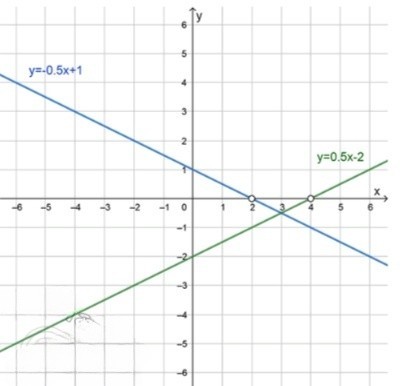
График функций:




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!