ГДЗ по Алгебре 9 Класс Номер 10 Дорофеев, Суворова — Подробные Ответы

Используя циркуль и линейку, отметьте на координатной прямой числа: $\sqrt{2}$, $-\sqrt{2}$, $\sqrt{2}-1$, $1-\sqrt{2}$, $-2\sqrt{2}$. Запишите данные числа в порядке возрастания.

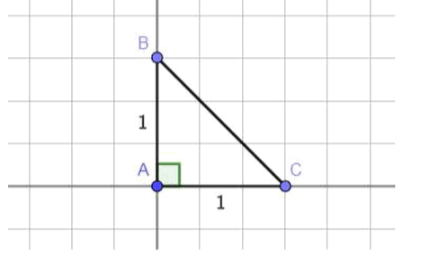
1)Для начала изобразим отрезок, длина которого равна $\sqrt{2}$:
– Проведем две перпендикулярные прямые, пересекающиеся в точке $A$;
– Из точки $A$ отложим единичный отрезок $AB$ на одну из прямых и единичный отрезок $AC$ на вторую прямую;
В прямоугольном треугольнике $ABC$ по теореме Пифагора:
$BC=\sqrt{A{B}^2+A{C}^2}=\sqrt{1+1}=\sqrt{2};$

2)Отметим искомые точки на координатной прямой:
– От точки $0$ при помощи циркуля, раствор которого равен длине отрезка $BC$, отложим отрезки длины $\sqrt{2}$ в левую и правую стороны, их вторые концы являются точками $-\sqrt{2}$ и $\sqrt{2}$ соответственно;
– Из точки $\sqrt{2}$ влево отложим единичный отрезок, его второй конец является точкой $\sqrt{2}-1$;
– Из точки $1$ влево отложим отрезок длины $\sqrt{2}$, его второй конец является точкой $1-\sqrt{2}$;
– Из точки $-\sqrt{2}$ влево отложим отрезок длины $\sqrt{2}$, его второй конец является точкой $-2\sqrt{2}$;

Ответ: $-2\sqrt{2}$; $-\sqrt{2}$; $1-\sqrt{2}$; $\sqrt{2}-1$; $\sqrt{2}$.

1)Для начала изобразим отрезок, длина которого равна $\sqrt{2}$:
– Проведем две перпендикулярные прямые, пересекающиеся в точке $A$. Эти прямые будут служить основой для построения единичных отрезков. Положим, что одна из прямых будет горизонтальной, а другая вертикальной. Точка $A$ будет являться их пересечением.
– Из точки $A$ отложим единичный отрезок $AB$ на одну из прямых (например, на горизонтальную) и единичный отрезок $AC$ на другую прямую (например, на вертикальную). Теперь мы получили прямоугольный треугольник $ABC$, где катеты $AB$ и $AC$ имеют длину 1.
В прямоугольном треугольнике $ABC$ по теореме Пифагора, которая утверждает, что сумма квадратов катетов равна квадрату гипотенузы, имеем:

$$BC=\sqrt{A{B}^2+A{C}^2}=\sqrt{1^2+1^2}=\sqrt{1+1}=\sqrt{2}$$

Таким образом, мы построили отрезок длины $\sqrt{2}$, который и будет искомым отрезком.

2)Отметим искомые точки на координатной прямой:
– От точки $0$ при помощи циркуля, раствор которого равен длине отрезка $BC$, отложим отрезки длины $\sqrt{2}$ в левую и правую стороны. В правую сторону отложим отрезок длины $\sqrt{2}$, и его второй конец будет точкой $\sqrt{2}$. В левую сторону отложим отрезок длины $\sqrt{2}$, и его второй конец будет точкой $-\sqrt{2}$. Таким образом, мы получаем точки $-\sqrt{2}$ и $\sqrt{2}$, которые являются решениями, соответствующими отложенным отрезкам.
– Из точки $\sqrt{2}$ влево отложим единичный отрезок. Это означает, что от точки $\sqrt{2}$ нужно отступить на единицу влево, и его второй конец будет точкой $\sqrt{2}-1$.
– Из точки $1$ влево отложим отрезок длины $\sqrt{2}$. Это означает, что от точки $1$ нужно отступить на $\sqrt{2}$ влево, и его второй конец будет точкой $1-\sqrt{2}$.
– Из точки $-\sqrt{2}$ влево отложим отрезок длины $\sqrt{2}$. Это означает, что от точки $-\sqrt{2}$ нужно отступить на $\sqrt{2}$ влево, и его второй конец будет точкой $-2\sqrt{2}$.

Ответ: $-2\sqrt{2}$; $-\sqrt{2}$; $1-\sqrt{2}$; $\sqrt{2}-1$; $\sqrt{2}$.