ГДЗ по Алгебре 9 Класс Номер 300 Дорофеев, Суворова — Подробные Ответы

Решите неравенство
а) $4x(x + 2) < 5$;

б) $(2x + 1)(x + 1) > 3$;

в) $3x(1 — x) \leqslant -6$;

г) $(1 — 2x)(1 — 3x) \leqslant 2$.

а) $4x(x + 2) < 5$:

$4x^2 + 8x — 5 < 0$;

$a = 4 > 0$, значит ветви направлены вверх;

2) Нули функции:

$4x^2 + 8x — 5 = 0$;

$D = 8^2 + 4 \cdot 4 \cdot 5 = 64 + 80 = 144$, тогда:

$x_1 = \frac{-8 — 12}{2 \cdot 4} = -2.5$ и $x_2 = \frac{-8 + 12}{2 \cdot 4} = 0.5$;

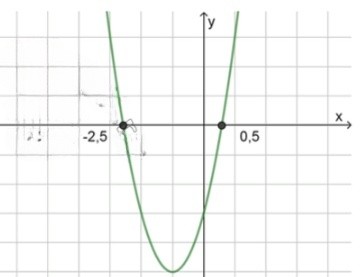
3) Схематический рисунок:

Ответ: $(-2.5; 0.5)$.

б) $(2x + 1)(x + 1) > 3$:

$2x^2 + 2x + x + 1 — 3 > 0$;

$2x^2 + 3x — 2 > 0$;

$a = 2 > 0$, значит ветви направлены вверх;

2) Нули функции:

$2x^2 + 3x — 2 = 0$;

$D = 3^2 + 4 \cdot 2 \cdot 2 = 9 + 16 = 25$, тогда:

$x_1 = \frac{-3 — 5}{2 \cdot 2} = -2$ и $x_2 = \frac{-3 + 5}{2 \cdot 2} = 0.5$;

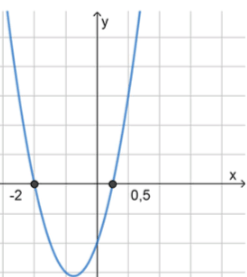
3) Схематический рисунок:

Ответ: $(- \infty; -2) \cup (0.5; +\infty)$.

в) $3x(1 — x) \leqslant -6$:

$-3x^2 + 3x + 6 \leqslant 0$;

$a = -3 < 0$, значит ветви направлены вниз;

2) Нули функции:

$-3x^2 + 3x + 6 = 0 \quad | : (-3)$;

$x^2 — x — 2 = 0$;

$D = 1^2 + 4 \cdot 2 = 1 + 8 = 9$, тогда:

$x_1 = \frac{1 — 3}{2} = -1$ и $x_2 = \frac{1 + 3}{2} = 2$;

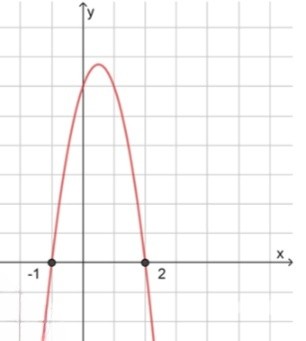
3) Схематический рисунок:

Ответ: $(- \infty; -1] \cup [2; +\infty)$.

г) $(1 — 2x)(1 — 3x) \leqslant 2$:

$1 — 3x — 2x + 6x^2 — 2 \leqslant 0$;

$6x^2 — 5x — 1 \leqslant 0$;

$a = 6 > 0$, значит ветви направлены вверх;

2) Нули функции:

$6x^2 — 5x — 1 = 0$;

$D = 5^2 + 4 \cdot 6 = 25 + 24 = 49$, тогда:

$x_1 = \frac{5 — 7}{2 \cdot 6} = -\frac{1}{6}$ и $x_2 = \frac{5 + 7}{2 \cdot 6} = 1$;

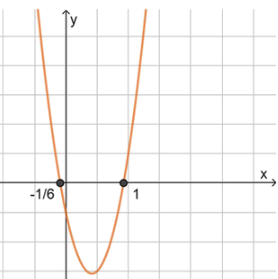
3) Схематический рисунок:

Ответ: $\left[-\frac{1}{6}; 1\right]$.

а) $4x(x + 2) < 5$:

Раскроем скобки:

$$4x(x + 2) = 4x^2 + 8x$$

Таким образом, неравенство становится:

$$4x^2 + 8x < 5$$

Переносим все в одну сторону:

$$4x^2 + 8x — 5 < 0$$

Рассмотрим соответствующее квадратное уравнение:

$$4x^2 + 8x — 5 = 0$$

Для нахождения корней используем дискриминант:

$$D = 8^2 — 4 \cdot 4 \cdot (-5) = 64 + 80 = 144$$

Корни уравнения:

$$x_1=\frac{-8-\sqrt{144}}{2\cdot 4}=\frac{-8-12}{8}=-\frac{20}{8}=-2.5,$$

$$x_1 = \frac{-8 — \sqrt{144}}{2 \cdot 4} = \frac{-8 — 12}{8} = -\frac{20}{8} = -2.5, \quad x_2 = \frac{-8 + \sqrt{144}}{2 \cdot 4} = \frac{-8 + 12}{8} = \frac{4}{8} = 0.5$$

Парабола с ветвями вверх (так как $a = 4 > 0$) пересекает ось $x$ в точках $x = -2.5$ и $x = 0.5$.

Для неравенства $4x^2 + 8x — 5 < 0$ функция будет отрицательной между этими корнями. Следовательно, решение неравенства:

$$x \in (-2.5; 0.5)$$

Ответ: $(-2.5; 0.5)$.

б) $(x + 8)(1 — x) > 3$:

Раскроем скобки:

$$(x + 8)(1 — x) = x — x^2 + 8 — 8x = -x^2 — 7x + 8$$

Таким образом, неравенство становится:

$$-x^2 — 7x + 8 > 3$$

Переносим все в одну сторону:

$$-x^2 — 7x + 8 — 3 > 0$$ $$-x^2 — 7x + 5 > 0$$

Рассмотрим соответствующее квадратное уравнение:

$$-x^2 — 7x + 5 = 0$$

Для нахождения корней используем дискриминант:

$$D = (-7)^2 — 4 \cdot (-1) \cdot 5 = 49 + 20 = 69$$

Корни уравнения:

$$x_1=\frac{-(-7)-\sqrt{69}}{2\cdot (-1)}=\frac{7-\sqrt{69}}{-2},$$

$$x_1 = \frac{-(-7) — \sqrt{69}}{2 \cdot (-1)} = \frac{7 — \sqrt{69}}{-2}, \quad x_2 = \frac{-(-7) + \sqrt{69}}{2 \cdot (-1)} = \frac{7 + \sqrt{69}}{-2}$$

Парабола с ветвями вниз (так как $a = -1 < 0$) пересекает ось $x$ в этих точках.

Для неравенства $-x^2 — 7x + 5 > 0$ функция будет положительной между этими корнями. Следовательно, решение неравенства:

$$x \in (x_1; x_2)$$

Ответ: $(x_1; x_2)$.

в) $2x(x + 3) \geqslant 0$:

Раскроем скобки:

$$2x(x + 3) = 2x^2 + 6x$$

Таким образом, неравенство становится:

$$2x^2 + 6x \geqslant 0$$

Рассмотрим соответствующее квадратное уравнение:

$$2x^2 + 6x = 0$$

Решим его:

$$2x(x + 3) = 0$$

Корни:

$$x_1 = 0, \quad x_2 = -3$$

Парабола с ветвями вверх (так как $a = 2 > 0$) пересекает ось $x$ в точках $x = -3$ и $x = 0$.

Для неравенства $2x^2 + 6x \geqslant 0$, функция будет положительной или равной нулю на интервалах $(-\infty; -3] \cup [0; +\infty)$.

Следовательно, решение неравенства:

$$x \in (-\infty; -3] \cup [0; +\infty)$$

Ответ: $(- \infty; -3] \cup [0; +\infty)$.

г) $0.5x(10 — x) < 0$:

Раскроем скобки:

$$0.5x(10 — x) = 5x — 0.5x^2$$

Таким образом, неравенство становится:

$$5x — 0.5x^2 < 0$$

Рассмотрим соответствующее квадратное уравнение:

$$5x — 0.5x^2 = 0$$

Решим его:

$$0.5x(10 — x) = 0$$

Корни:

$$x_1 = 0, \quad x_2 = 10$$

Парабола с ветвями вниз (так как $a = -0.5 < 0$) пересекает ось $x$ в точках $x = 0$ и $x = 10$. Для неравенства $5x — 0.5x^2 < 0$,

функция будет отрицательной между этими корнями. Следовательно, решение неравенства:

$$x \in (0; 10)$$

Ответ: $(0; 10)$.