ГДЗ по Алгебре 9 Класс Номер 200 Дорофеев, Суворова — Подробные Ответы

Составьте таблицу значений функции и постройте график (посмотрите, чтобы на графике была вершина и было ясно направление ветвей):

а) $y=x^2-5x+4;$
б) $y=-\frac{1}{2}{x}^2+2x\mathrm{.}$

Имеет ли функция наименьшее или наибольшее значение, и чему оно равно? При каком $x$ функция принимает это значение?

$$

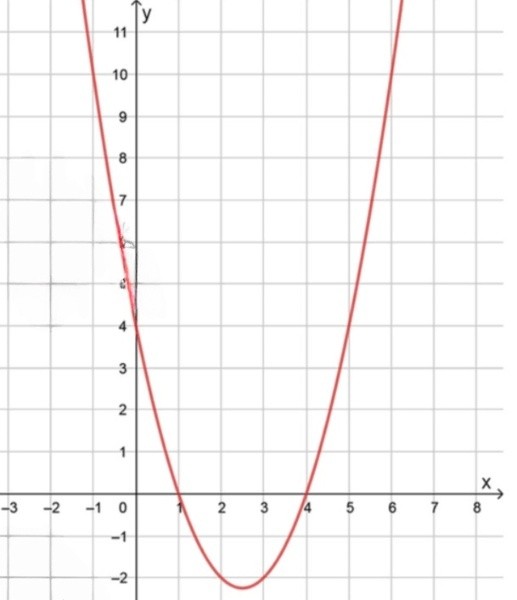
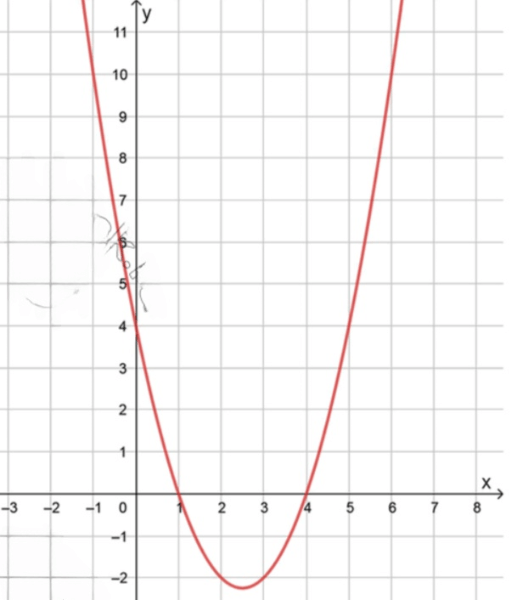
Имеет наименьшее значение: $y_{\text{min}}=-2,25$ при $x=2,5;$

б) $y=-\frac{1}{2}{x}^2+2x:$

$y = x^2 — 5x + 4:$

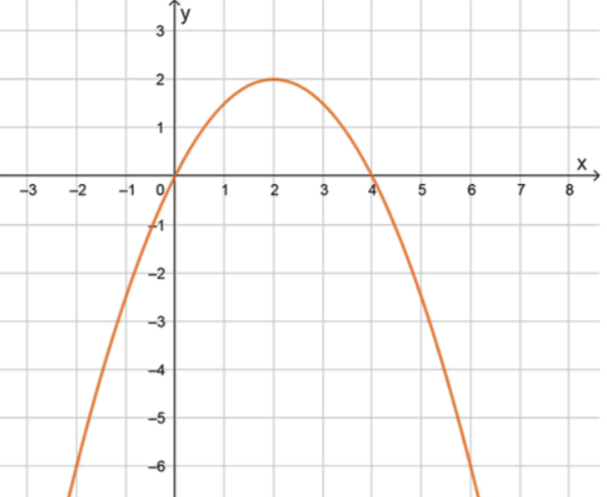
Имеет наибольшее значение: $y_{\text{max}}=2$ при $x=2;$

а) $y=x^2-5x+4:$

Для нахождения наименьшего значения функции $y=x^2-5x+4$ используем формулу для абсциссы вершины параболы. Функция является квадратичной, и ее график представляет собой параболу, ветви которой направлены вверх, так как коэффициент при $x^2$ положительный.

Для нахождения абсциссы вершины (значения $x$, при котором достигается наименьшее значение функции), используем формулу:

$$x=\frac{-b}{2a}$$

где $a=1$, $b=-5$. Подставляем значения:

$$x=\frac{-(-5)}{2(1)}=\frac{5}{2}=2,5$$

Теперь подставляем значение $x=2,5$ в исходную функцию для нахождения значения $y$:

$$y=(2,5{)}^2-5(2,5)+4=6,25-12,5+4=-2,25$$

Таким образом, наименьшее значение функции равно $y_{\text{min}}=-2,25$, и оно достигается при $x=2,5$.

График функции пересекает ось $x$ в точках, где $y=0$. Чтобы найти эти точки, решим уравнение:

$$x^2-5x+4=0$$

Решим квадратное уравнение с помощью формулы:

$$x=\frac{-(-5)\pm \sqrt{(-5{)}^2-4(1)(4)}}{2(1)}=\frac{5\pm \sqrt{25-16}}{2}=\frac{5\pm \sqrt{9}}{2}=\frac{5\pm 3}{2}$$

Таким образом, получаем два корня:

$$x=\frac{5+3}{2}=4\text{или}x=\frac{5-3}{2}=1$$

График пересекает ось $x$ в точках $x=1$ и $x=4$.

б) $y=-\frac{1}{2}{x}^2+2x:$

Для нахождения наибольшего значения функции $y=-\frac{1}{2}{x}^2+2x$ используем формулу для абсциссы вершины параболы. Здесь коэффициент при $x^2$ отрицательный, значит, парабола открывается вниз, и функция будет иметь наибольшее значение в вершине.

Используем ту же формулу для нахождения $x$-координаты вершины:

$$x=\frac{-b}{2a}$$

где $a=-\frac{1}{2}$, $b=2$. Подставляем значения:

$$x=\frac{-2}{2(-\frac{1}{2})}=\frac{-2}{-1}=2$$

Теперь подставляем $x=2$ в исходную функцию для нахождения значения $y$:

$$y=-\frac{1}{2}(2{)}^2+2(2)=-\frac{1}{2}(4)+4=-2+4=2$$

Таким образом, наибольшее значение функции равно $y_{\text{max}}=2$, и оно достигается при $x=2$.

Чтобы найти, пересекает ли график функции прямую $y=0$, решим уравнение:

$$-\frac{1}{2}{x}^2+2x=0$$

Вынесем общий множитель:

$$x(-\frac{1}{2}x+2)=0$$

Таким образом, получаем два корня:

$$x=0\text{или}-\frac{1}{2}x+2=0$$

Решаем второе уравнение:

$$-\frac{1}{2}x+2=0\Rightarrow \frac{1}{2}x=2\Rightarrow x=4$$

График пересекает ось $x$ в точках $x=0$ и $x=4$.