ГДЗ по Алгебре 9 Класс Это Надо Знать Глава 3 Номер 8 Дорофеев, Суворова — Подробные Ответы

На примере системы $\begin{cases} x^2 + y^2 = 9 \\ x + y = 2 \end{cases}$ покажите, в чём состоит графический способ решения системы двух уравнений с двумя переменными.

$\begin{cases} x^2 + y^2 = 9 \\ x + y = 2 \end{cases}$ $=>$ $\begin{cases} x^2 + y^2 = 9 \\ y = 2 — x \end{cases}$;

$x^2 + y^2 = 9$ — уравнение окружности:
$x_0 = 0$ и $y_0 = 0$, $R = \sqrt{9} = 3$;

$y = 2 — x$ — уравнение прямой:

$$\begin{array}{|c|c|c|} \hline x & 0 & 2 \\ \hline y & 2 & 0 \\ \hline \end{array}$$

3) Графики функций:

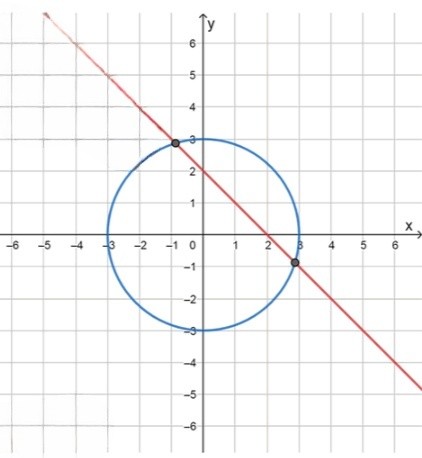
Графики функций пересекаются в двух точках:
$(-0,9; 2,9)$ и $(2,9; -0,9)$.

$\begin{cases} x^2 + y^2 = 9 \\ x + y = 2 \end{cases}$ $=>$ $\begin{cases} x^2 + y^2 = 9 \\ y = 2 — x \end{cases}$;

1) Рассмотрим уравнение $x^2 + y^2 = 9$. Это уравнение описывает окружность с центром в точке $(0, 0)$ и радиусом 3, так как его можно записать в стандартной форме уравнения окружности:

$$x^2 + y^2 = R^2,$$

где $R$ — радиус окружности. В данном случае $R = \sqrt{9} = 3$. Таким образом, у нас есть окружность с центром в начале координат, радиусом 3. Параметры окружности:

$$x_0 = 0, \quad y_0 = 0, \quad R = 3.$$

2) Рассмотрим уравнение $x + y = 2$. Это уравнение представляет собой прямую с угловым коэффициентом $-1$ и сечением с осью $y$ в точке $(0, 2)$. Чтобы выразить $y$ через $x$, решим его относительно $y$:

$$y = 2 — x.$$

Это уравнение прямой, которое можно записать в виде $y = -x + 2$. Для удобства построения графика выберем несколько значений $x$ и найдем соответствующие значения $y$. Например:

• Когда $x = 0$, $y = 2 — 0 = 2$.
• Когда $x = 2$, $y = 2 — 2 = 0$.

Таким образом, у нас есть две точки на прямой: $(0, 2)$ и $(2, 0)$.

3) Теперь построим графики этих двух функций. График функции $x^2 + y^2 = 9$ — это окружность с радиусом 3, а график функции $y = 2 — x$ — это прямая с угловым коэффициентом $-1$. Эти два графика пересекаются в двух точках, что подтверждает, что система уравнений имеет два решения.

Для нахождения точек пересечения подставим $y = 2 — x$ во второе уравнение системы $x^2 + y^2 = 9$:

$$x^2 + (2 — x)^2 = 9.$$

Раскроем скобки:

$$x^2 + (4 — 4x + x^2) = 9,$$ $$2x^2 — 4x + 4 = 9.$$

Теперь перенесем 9 в левую часть уравнения:

$$2x^2 — 4x + 4 — 9 = 0,$$ $$2x^2 — 4x — 5 = 0.$$

Решим это квадратное уравнение с помощью дискриминанта. Для уравнения $ax^2 + bx + c = 0$, дискриминант $D$ равен:

$$D = b^2 — 4ac.$$

В нашем случае $a = 2$, $b = -4$, $c = -5$. Подставим в формулу:

$$D = (-4)^2 — 4 \cdot 2 \cdot (-5) = 16 + 40 = 56.$$

Теперь находим корни уравнения:

$$x = \frac{-(-4) \pm \sqrt{56}}{2 \cdot 2} = \frac{4 \pm \sqrt{56}}{4}.$$

Корень из 56 можно упростить как $\sqrt{56} = 2\sqrt{14}$, тогда:

$$x = \frac{4 \pm 2\sqrt{14}}{4} = 1 \pm \frac{\sqrt{14}}{2}.$$

Таким образом, мы получаем два значения для $x$:

$$x_1 = 1 + \frac{\sqrt{14}}{2}, \quad x_2 = 1 — \frac{\sqrt{14}}{2}.$$

Теперь, подставив эти значения в уравнение $y = 2 — x$, находим соответствующие значения $y$. Для $x_1$:

$$y_1 = 2 — \left(1 + \frac{\sqrt{14}}{2}\right) = 1 — \frac{\sqrt{14}}{2},$$

и для $x_2$:

$$y_2 = 2 — \left(1 — \frac{\sqrt{14}}{2}\right) = 1 + \frac{\sqrt{14}}{2}.$$

Ответ: точки пересечения графиков функций: $\left(1 + \frac{\sqrt{14}}{2}, 1 — \frac{\sqrt{14}}{2}\right)$ и $\left(1 — \frac{\sqrt{14}}{2}, 1 + \frac{\sqrt{14}}{2}\right)$.