ГДЗ по Алгебре 9 Класс Это Надо Знать Глава 2 Номер 8 Дорофеев, Суворова — Подробные Ответы

Как из параболы $y = ax^2$ получить параболу $y = a(x + p)^2 + q$?

Приведите пример. Сделайте схематический рисунок.

Чтобы из параболы $y = ax^2$ получить параболу $y = a(x + p)^2 + q$, нужно выполнить два последовательных переноса:

• Вдоль оси $x$ на $|p|$ единиц (влево, если $p > 0$, или вправо, если $p < 0$);
• Вдоль оси $y$ на $|q|$ единиц (вверх, если $q > 0$, или вниз, если $q < 0$).

При этом вершина параболы окажется в точке $(-p; q)$.

Например:
Чтобы из параболы $y = 2x^2$ получить параболу $y = 2(x — 3)^2 + 2$, нужно:

• Перенести параболу $y = 2x^2$ вдоль оси $x$ вправо на 3 единицы;
• Перенести полученную параболу вдоль оси $y$ вверх на 2 единицы.

При этом вершина параболы окажется в точке $(3; 2)$.

Схематический рисунок:

Чтобы из параболы $y = ax^2$ получить параболу $y = a(x + p)^2 + q$, необходимо выполнить два геометрических преобразования графика: сначала сдвиг по горизонтали (вдоль оси $x$), затем сдвиг по вертикали (вдоль оси $y$).

Первое преобразование — замена $x$ на $x + p$:

— Если заменить $x$ на $x + p$, получится выражение $y = a(x + p)^2$.
— Это приводит к параллельному переносу графика вдоль оси $x$.
— Направление переноса зависит от знака $p$:

• если $p > 0$, то график сдвигается влево на $p$ единиц, так как каждое значение $x$ в новой функции должно быть на $p$ меньше, чтобы получить ту же $y$, что и в исходной функции;
• если $p < 0$, то график сдвигается вправо на $|p|$, поскольку $x + p$ становится меньше, и чтобы компенсировать это, $x$ нужно увеличить, то есть график уходит вправо.

Таким образом, результатом первого преобразования будет парабола с вершиной в точке $(-p;\ 0)$.

Второе преобразование — добавление константы $q$ к значению функции:

— После горизонтального сдвига, если к выражению $y = a(x + p)^2$ прибавить $q$, получается $y = a(x + p)^2 + q$.
— Это означает, что каждое значение функции увеличивается или уменьшается на $q$:

• если $q > 0$, то весь график поднимается вверх на $q$ единиц,
• если $q < 0$, то график опускается вниз на $|q|$ единиц.

Итоговая вершина параболы после обоих преобразований будет находиться в точке $(-p;\ q)$.

Обобщённый алгоритм построения графика функции $y = a(x + p)^2 + q$ из графика $y = ax^2$:

Выполнить горизонтальный сдвиг:
— если $p > 0$, сдвинуть график влево на $p$ единиц;
— если $p < 0$, сдвинуть график вправо на $|p|$ единиц.

Затем выполнить вертикальный сдвиг:
— если $q > 0$, сдвинуть график вверх на $q$ единиц;
— если $q < 0$, сдвинуть график вниз на $|q|$ единиц.

Пример:

Пусть дана функция $y = 2x^2$. Построим по ней график функции $y = 2(x — 3)^2 + 2$.

Здесь:

— $a = 2$ (отвечает за ширину и направление ветвей параболы);
— $p = -3$, так как $x — 3 = x + (-3)$, следовательно, $p < 0$;
— $q = 2$, следовательно, сдвиг по $y$ вверх на 2 единицы.

Шаги построения:

От графика функции $y = 2x^2$ переходим к $y = 2(x — 3)^2$:
— $p = -3$, следовательно, график сдвигается вправо на 3 единицы.
— Вершина новой параболы — точка $(3;\ 0)$.

Затем добавляем $q = 2$, получаем функцию $y = 2(x — 3)^2 + 2$:
— график сдвигается вверх на 2 единицы.
— Вершина окончательной параболы — точка $(3;\ 2)$.

То есть:

— График $y = 2x^2$: вершина в точке $(0;\ 0)$;
— График $y = 2(x — 3)^2$: вершина в точке $(3;\ 0)$;
— График $y = 2(x — 3)^2 + 2$: вершина в точке $(3;\ 2)$.

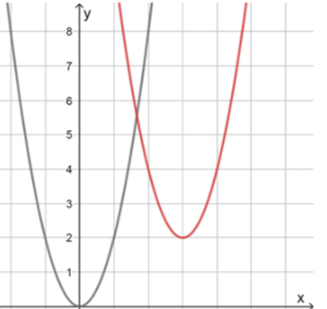
Схематическое изображение:

— Первый график (исходный) — синяя парабола с вершиной в начале координат;
— Второй график (после сдвига по $x$) — зеленая парабола, сдвинутая вправо на 3;
— Третий график (после сдвига по $y$) — красная парабола, сдвинутая вверх на 2.

Таким образом, функция $y = a(x + p)^2 + q$ задаёт параболу, полученную из $y = ax^2$ путём переноса вершины в точку $(-p;\ q)$, с сохранением направления и степени сжатия/растяжения в зависимости от $a$.