ГДЗ по Алгебре 9 Класс Это Надо Знать Глава 2 Номер 7 Дорофеев, Суворова — Подробные Ответы

Как из параболы $y = ax^2$ получить параболу $y = a(x + p)^2$?

Продемонстрируйте свой ответ схематическими рисунками.

Чтобы из параболы $y = ax^2$ получить параболу $y = a(x + p)^2$, ее нужно перенести вдоль оси $x$:

влево на отрезок длины $p$, если $p > 0$;

вправо на отрезок длины $|p|$, если $p < 0$.

При этом вершина параболы окажется в точке $(-p; 0)$.

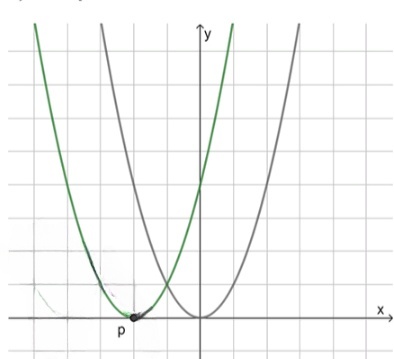
1) Если $p > 0$:

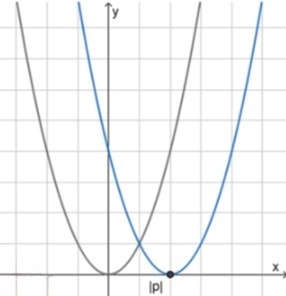
2) Если $p < 0$:

Чтобы из параболы $y = ax^2$ получить параболу $y = a(x + p)^2$, нужно выполнить параллельный перенос графика вдоль оси абсцисс (оси $x$).

Формула $y = a(x + p)^2$ является результатом замены переменной: в исходной функции $y = ax^2$ вместо $x$ подставлено выражение $x + p$. То есть, каждый $x$ заменяется на $x + p$, и тем самым график функции смещается в противоположную сторону по оси $x$ на величину $p$.

Рассмотрим подробнее:

Если $p > 0$, то:

— функция принимает вид $y = a(x + p)^2$;
— для любого значения $x$, новое значение $x + p$ больше $x$;
— это означает, что чтобы сохранить те же значения $y$, необходимо уменьшить $x$ на $p$;
— значит, график параболы сдвигается влево на расстояние $p$.

Если $p < 0$, то:

— функция принимает вид $y = a(x + p)^2$, но теперь $p$ отрицательно;
— следовательно, $x + p < x$, то есть значения $x$ должны быть больше, чтобы сохранить те же $y$;
— значит, график параболы сдвигается вправо на расстояние $|p|$.

Геометрический смысл:
— Вершина исходной параболы $y = ax^2$ находится в начале координат, в точке $(0, 0)$;
— после подстановки $x + p$, вершина смещается в точку $x = -p$, а значение функции там по-прежнему равно нулю:
$y = a(-p + p)^2 = a \cdot 0 = 0$;
— значит, новая вершина находится в точке $(-p;\ 0)$.

Итог:

— Если $p > 0$, график параболы $y = ax^2$ сдвигается влево на $p$ единиц и превращается в параболу $y = a(x + p)^2$;
— Если $p < 0$, график параболы $y = ax^2$ сдвигается вправо на $|p|$ единиц и превращается в ту же самую форму $y = a(x + p)^2$, но со сдвигом вправо.

Вершина новой параболы — это точка $(-p;\ 0)$, и ось симметрии параболы теперь — прямая $x = -p$.

Графическая иллюстрация:

1) Если $p > 0$, например $p = 2$:
График $y = ax^2$ сдвигается влево на 2 единицы → новая вершина в точке $(-2, 0)$:
$y = a(x + 2)^2$

2) Если $p < 0$, например $p = -3$:
График $y = ax^2$ сдвигается вправо на 3 единицы → новая вершина в точке $(3, 0)$:
$y = a(x — 3)^2$

Таким образом, запись $y = a(x + p)^2$ указывает на горизонтальный сдвиг параболы $y = ax^2$, при котором каждая точка графика перемещается на $-p$ по оси $x$, и вершина оказывается в точке $(-p; 0)$.