ГДЗ по Алгебре 9 Класс Это Надо Знать Глава 2 Номер 6 Дорофеев, Суворова — Подробные Ответы

Как из параболы $y = ax^2$ получить параболу $y = ax^2 + q$?

Продемонстрируйте свой ответ схематическими рисунками.

Чтобы из параболы $y = ax^2$ получить параболу $y = ax^2 + q$, ее требуется перенести вдоль оси $y$:

вверх на отрезок длины $q$, если $q > 0$;

вниз на отрезок длины $\mathrm{}$$|q|$, если $q < 0$.

При этом вершина параболы окажется в точке $(0; q)$.

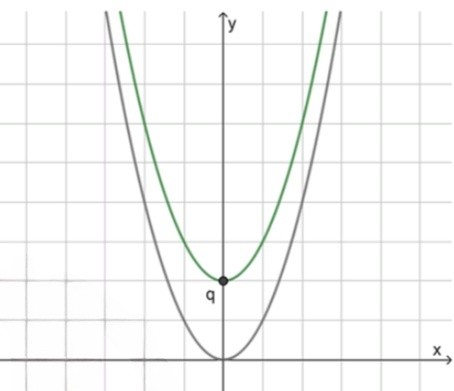
1) Если $q > 0$:

2) Если $q < 0$:

Чтобы из параболы $y = ax^2$ получить параболу $y = ax^2 + q$, необходимо изменить её положение на графике вдоль оси $y$. Эта трансформация представляет собой сдвиг графика параболы вверх или вниз в зависимости от знака $q$.

Если $q > 0$, то парабола сдвигается вверх на величину $q$. Это означает, что каждый $y$-координат точек графика функции $y = ax^2$ будет увеличен на $q$, то есть для всех $x$ новое значение функции будет равно $y = ax^2 + q$.
Таким образом, парабола перемещается вверх на отрезок длины $q$, и её вершина будет находиться в точке $(0, q)$.

Если $q < 0$, то парабола сдвигается вниз на величину $|q|$. В этом случае $y$-координаты всех точек параболы будут уменьшены на $|q|$, что приводит к сдвигу графика вниз на расстояние $|q|$. Вершина параболы также перемещается в точку $(0, q)$, но теперь $q$ будет отрицательным, что означает, что вершина окажется ниже оси $x$.

В обоих случаях ось симметрии параболы остаётся неизменной, то есть остаётся вдоль прямой $x = 0$. Это связано с тем, что в функции $y = ax^2 + q$ не меняется коэффициент $a$, который отвечает за форму параболы, только сдвигается её положение по вертикали.

Таким образом:

При $q > 0$ график параболы сдвигается вверх на величину $q$, и вершина перемещается в точку $(0, q)$.

При $q < 0$ график параболы сдвигается вниз на величину $|q|$, и вершина также перемещается в точку $(0, q)$.

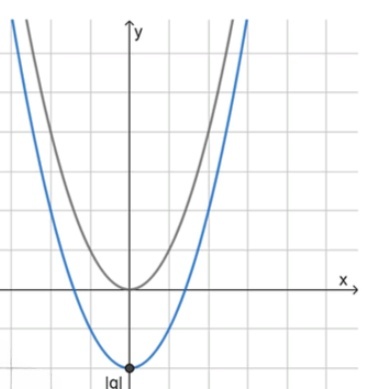
1) Если $q > 0$:

График функции $y = ax^2 + q$ будет расположён выше графика функции $y = ax^2$ на величину $q$, и вершина параболы будет в точке $(0, q)$. Например, для $a = 1$ и $q = 2$, функция $y = x^2 + 2$ будет сдвинута вверх на 2 единицы.

2) Если $q < 0$:

График функции $y = ax^2 + q$ будет расположён ниже графика функции $y = ax^2$ на величину $|q|$, и вершина параболы будет в точке $(0, q)$. Например, для $a = 1$ и $q = -2$, функция $y = x^2 — 2$ будет сдвинута вниз на 2 единицы.