ГДЗ по Алгебре 9 Класс Это Надо Знать Глава 2 Номер 5 Дорофеев, Суворова — Подробные Ответы

Постройте график функции $y = ax^2$:

а) при $a = \frac{1}{2}$;
б) при $a = -2$.

Опишите в каждом случае свойства функции.

Функция: $y = ax^2$;

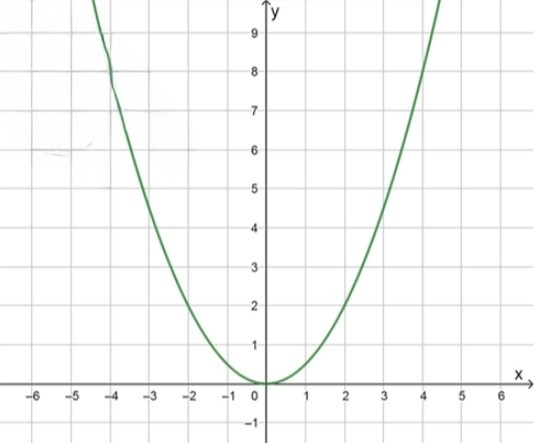
а) При $a = \frac{1}{2}$ получим функцию $y = \frac{1}{2}x^2$:
$a > 0$, значит ветви параболы направлены вверх;
Вершина параболы находится в точке $(0; 0)$;
Уравнение оси симметрии: $x = 0$;
Координаты некоторых точек:

$$\begin{array}{|c|c|c|c|c|} \hline x & -4 & -2 & 2 & 4 \\ \hline y & 8 & 2 & 2 & 8 \\ \hline \end{array}$$

Функция возрастает при $x > 0$;
Функция убывает при $x < 0$;
$y > 0$ при $x \neq 0$;
Наименьшее значение функции: $y = 0$ при $x = 0$;

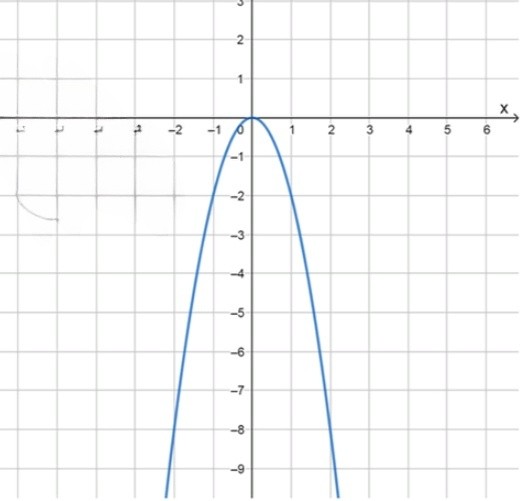
б) При $a = -2$ получим функцию $y = -2x^2$:
$a < 0$, значит ветви параболы направлены вниз;
Вершина параболы находится в точке $(0; 0)$;
Уравнение оси симметрии: $x = 0$;
Координаты некоторых точек:

$$\begin{array}{|c|c|c|c|c|} \hline x & -2 & -1 & 1 & 2 \\ \hline y & -8 & -2 & -2 & -8 \\ \hline \end{array}$$

Функция возрастает при $x < 0$;
Функция убывает при $x > 0$;
$y < 0$ при $x \neq 0$;
Наибольшее значение функции: $y = 0$ при $x = 0$.

Функция: $y = ax^2$;

а) При $a = \frac{1}{2}$ получим функцию $y = \frac{1}{2}x^2$:

$a > 0$, значит ветви параболы направлены вверх. Это означает, что парабола будет открываться вверх, и её график будет подниматься вверх по мере того, как $x$ удаляется от нуля в обе стороны. Парабола будет симметрична относительно вертикальной оси $x = 0$, которая является её осью симметрии.

Вершина параболы находится в точке $(0, 0)$. Это свойство следствие того, что в функции $y = ax^2$ нет линейного и константного членов, и вершина всегда расположена в начале координат, поскольку минимальное значение функции происходит при $x = 0$.

Уравнение оси симметрии: $x = 0$. Это вертикальная прямая, которая проходит через вершину параболы и разделяет её на две симметричные части. В данном случае ось симметрии совпадает с осью $y$.

Координаты некоторых точек функции для $x = -4, -2, 2, 4$:

$$\begin{array}{|c|c|c|c|c|} \hline x & -4 & -2 & 2 & 4 \\ \hline y & 8 & 2 & 2 & 8 \\ \hline \end{array}$$

Эти значения показывают, что на одинаковых расстояниях от оси симметрии, то есть при $x = -4$ и $x = 4$, а также при $x = -2$ и $x = 2$, функция принимает одинаковые значения $y$, что подтверждает симметричность графика параболы.

Функция возрастает при $x > 0$. Это объясняется тем, что, так как парабола открывается вверх, для положительных значений $x$, функция $y = \frac{1}{2}x^2$ будет увеличиваться с ростом $x$.

Функция убывает при $x < 0$. Для отрицательных значений $x$, так как парабола симметрична, значение функции будет уменьшаться по мере того, как $x$ приближается к нулю.

$y > 0$ при $x \neq 0$. Это свойство параболы, поскольку $y = \frac{1}{2}x^2$ всегда будет положительным для всех $x \neq 0$, так как квадрат любого числа всегда положителен.

Наименьшее значение функции: $y = 0$ при $x = 0$. Это минимальное значение функции, поскольку парабола открывается вверх и вершина параболы находится в точке $(0, 0)$.

б) При $a = -2$ получим функцию $y = -2x^2$:

$a < 0$, значит ветви параболы направлены вниз. В этом случае парабола будет открываться вниз, и её график будет опускаться по мере того, как $x$ удаляется от нуля в обе стороны.

Вершина параболы находится в точке $(0, 0)$. Это аналогично предыдущему случаю, так как функция $y = -2x^2$ также не имеет линейных и константных членов, и её минимальное значение (в случае $a < 0$, это максимальное значение функции) происходит в начале координат.

Уравнение оси симметрии: $x = 0$. Как и в предыдущем случае, ось симметрии параболы совпадает с осью $y$, так как парабола симметрична относительно вертикальной прямой, проходящей через её вершину.

Координаты некоторых точек функции для $x = -2, -1, 1, 2$:

$$\begin{array}{|c|c|c|c|c|} \hline x & -2 & -1 & 1 & 2 \\ \hline y & -8 & -2 & -2 & -8 \\ \hline \end{array}$$

Как и в предыдущем случае, график функции симметричен относительно оси $y$, и для одинаковых по величине значений $x$ с разными знаками (например, $x = -2$ и $x = 2$) значения функции одинаковы.

Функция возрастает при $x < 0$. Парабола, направленная вниз, будет возрастать (становиться менее отрицательной) по мере уменьшения $x$ от нуля.

Функция убывает при $x > 0$. Для положительных значений $x$, функция будет убывать, так как парабола открывается вниз, и значения $y$ будут становиться всё более отрицательными.

$y < 0$ при $x \neq 0$. Парабола с $a < 0$ всегда даёт отрицательные значения $y$, за исключением вершины, где $y = 0$.

Наибольшее значение функции: $y = 0$ при $x = 0$. Вершина параболы, где достигается наибольшее значение функции, находится в точке $(0, 0)$, так как при $a < 0$ парабола открывается вниз и наибольшее значение функции будет на вершине.