ГДЗ по Алгебре 9 Класс Это Надо Знать Глава 1 Номер 9 Дорофеев, Суворова — Подробные Ответы

Покажите на примерах систем $\begin{cases} x < 2 \\ x < 3 \end{cases}$ и $\begin{cases} x > 2 \\ x < 3 \end{cases}$, как с помощью координатной прямой находят множество решений системы неравенств.

Отметим на координатной прямой множества решений для первого и второго неравенства; множество решений системы будет являться их пересечением:

1)$\begin{cases} x < 2 \\ x < 3 \end{cases}$:

Ответ: $x \in (-\infty; 2)$.

2)$\begin{cases} x > 2 \\ x < 3 \end{cases}$:

Ответ: $x \in (2; 3)$.

Отметим на координатной прямой множества решений для каждого неравенства в составе системы. Затем найдём их пересечение — это и будет множество решений всей системы.

1)$\begin{cases} x < 2 \\ x < 3 \end{cases}$:

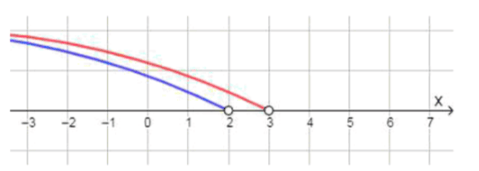
Первое неравенство: $x < 2$. Это означает, что решениями являются все действительные числа, которые строго меньше $2$. На координатной прямой эта область изображается открытым кругом в точке $2$ и стрелкой, направленной влево до минус бесконечности.

Второе неравенство: $x < 3$. Здесь решениями будут все числа, строго меньшие $3$. На координатной прямой — открытый круг в точке $3$ и стрелка влево.

Теперь найдём пересечение этих двух множеств. Обе стрелки направлены влево, но границы разные: первая — в точке $2$, вторая — в точке $3$. Пересекаются они в области до $2$, так как $x < 2$ строже. Следовательно:

Ответ: $x \in (-\infty; 2)$.

2)$\begin{cases} x > 2 \\ x < 3 \end{cases}$:

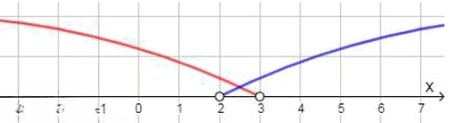
Первое неравенство: $x > 2$. Решения — все числа строго больше $2$. На координатной прямой — открытый круг в точке $2$ и стрелка вправо.

Второе неравенство: $x < 3$. Решения — все числа строго меньше $3$. На координатной прямой — открытый круг в точке $3$ и стрелка влево.

Пересечение этих двух множеств лежит строго между точками $2$ и $3$, не включая ни одну из границ, так как оба неравенства строгие. Это интервал:

Ответ: $x \in (2; 3)$.