ГДЗ по Алгебре 9 Класс Это Надо Знать Глава 1 Номер 2 Дорофеев, Суворова — Подробные Ответы

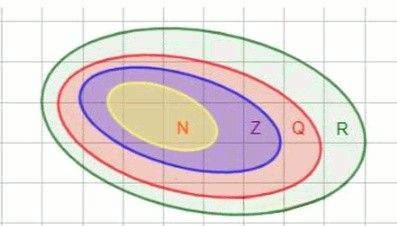
Показать схематические соотношения между множествами натуральных, целых, рациональных и действительных чисел:

Множество натуральных чисел ($\mathbb{N}$) включается в множество целых чисел ($\mathbb{Z}$).

Множество целых чисел ($\mathbb{Z}$) включается в множество рациональных чисел ($\mathbb{Q}$).

Множество рациональных чисел ($\mathbb{Q}$) включается в множество действительных чисел ($\mathbb{R}$).

Вставить знак $\in$ или $\notin$ так, чтобы получилось верное высказывание:

$-3 \notin \mathbb{N}$, $-3 \in \mathbb{Z}$, $-3 \in \mathbb{R}$.

$10 \in \mathbb{N}$, $10 \in \mathbb{Z}$, $10 \in \mathbb{R}$.

$\sqrt{2} \notin \mathbb{N}$, $\sqrt{2} \notin \mathbb{Z}$, $\sqrt{2} \in \mathbb{R}$.

Множество действительных чисел включает множество всех рациональных чисел;
Множество рациональных чисел включает множество всех целых чисел;
Множество целых чисел включает множество всех натуральных чисел;

$-3 \notin \mathbb{N}$; $-3 \in \mathbb{Z}$; $-3 \in \mathbb{R}$;
$10 \in \mathbb{N}$; $10 \in \mathbb{Z}$; $10 \in \mathbb{R}$;
$\sqrt{2} \notin \mathbb{N}$; $\sqrt{2} \notin \mathbb{Z}$; $\sqrt{2} \in \mathbb{R}$.

Множество действительных чисел обозначается символом $\mathbb{R}$ и включает в себя все числа, которые можно изобразить на числовой прямой. Это множество объединяет два основных подкласса чисел: рациональные и иррациональные. Таким образом, любые рациональные числа также являются действительными.

Множество рациональных чисел обозначается $\mathbb{Q}$ и состоит из всех чисел, представимых в виде дроби $\frac{m}{n}$, где $m \in \mathbb{Z}$, $n \in \mathbb{N}$. Это означает, что каждое целое число также можно выразить как дробь (например, $5 = \frac{5}{1}$), а значит, множество целых чисел входит в множество рациональных.

Множество целых чисел обозначается $\mathbb{Z}$ и включает как положительные, так и отрицательные числа и ноль: $\ldots, -3, -2, -1, 0, 1, 2, 3, \ldots$. Это множество шире, чем множество натуральных чисел, потому что содержит также отрицательные значения и ноль (в некоторых определениях).

Множество натуральных чисел обозначается $\mathbb{N}$. В разных странах и учебниках оно может включать либо только положительные числа $\{1, 2, 3, \ldots\}$, либо также и ноль $\{0, 1, 2, \ldots\}$. Однако в большинстве школьных курсов под $\mathbb{N}$ понимаются положительные целые числа без нуля.

Итак, последовательность включения множеств следующая:

$$\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}$$

Проверим принадлежность конкретных чисел к этим множествам:

1. Число $-3$ — это отрицательное целое число. Оно не является натуральным, так как в $\mathbb{N}$ входят только положительные числа. Однако оно принадлежит к целым ($\mathbb{Z}$), так как это число без дробной части, и, следовательно, принадлежит также к рациональным ($\mathbb{Q}$, так как $-3 = \frac{-3}{1}$) и действительным ($\mathbb{R}$).

$$-3 \notin \mathbb{N}; \quad -3 \in \mathbb{Z}; \quad -3 \in \mathbb{R}$$

2. Число $10$ — это положительное целое число. Оно принадлежит множеству натуральных чисел, так как $10 > 0$, значит также принадлежит множеству целых, рациональных и действительных.

$$10 \in \mathbb{N}; \quad 10 \in \mathbb{Z}; \quad 10 \in \mathbb{R}$$

3. Число $\sqrt{2}$ — это корень из натурального числа, который не может быть выражен в виде дроби с целыми числителем и знаменателем. Следовательно, $\sqrt{2}$ — иррациональное число. Оно не принадлежит ни множеству натуральных, ни множеству целых, ни множеству рациональных. Но оно входит в состав действительных чисел, так как его можно изобразить на числовой прямой.

$$\sqrt{2} \notin \mathbb{N}; \quad \sqrt{2} \notin \mathbb{Z}; \quad \sqrt{2} \in \mathbb{R}$$