ГДЗ по Алгебре 9 Класс Это Надо Уметь Глава 5 Номер 2 Дорофеев, Суворова — Подробные Ответы

Вернитесь к задаче 748 и постройте гистограмму частот для 2010 г.

1) Таблица значений:

2) Гистограмма частот для 2010 года:

1) Таблица значений:

В данной таблице представлен статистический ряд, отражающий, сколько дней в течение года наблюдалась температура воздуха, попадающая в определённый интервал значений. Всего зафиксировано 5 интервалов температур. В первом интервале $14 – 18^\circ C$ было только 1 день, во втором интервале $18 – 22^\circ C$ уже 6 дней, в третьем интервале $22 – 26^\circ C$ наибольшее количество — 15 дней, в четвёртом интервале $26 – 30^\circ C$ зафиксировано 3 дня и в пятом интервале $30 – 34^\circ C$ наблюдалось 5 дней. Такая таблица является частотным распределением, где каждому интервалу соответствует его абсолютная частота.

Для удобства анализа данных используется не только абсолютная, но и относительная частота. Относительная частота вычисляется по формуле $f_i = \frac{n_i}{N}$, где $n_i$ — количество наблюдений в интервале, $N$ — общее количество наблюдений. В данном случае общее количество дней равно $N = 1 + 6 + 15 + 3 + 5 = 30$. Тогда для каждого интервала:
для $14 – 18^\circ C$: $f_1 = \frac{1}{30} \approx 0,033$;
для $18 – 22^\circ C$: $f_2 = \frac{6}{30} = 0,2$;
для $22 – 26^\circ C$: $f_3 = \frac{15}{30} = 0,5$;
для $26 – 30^\circ C$: $f_4 = \frac{3}{30} = 0,1$;
для $30 – 34^\circ C$: $f_5 = \frac{5}{30} \approx 0,167$.

Таким образом, относительные частоты показывают, что половина всех дней (50%) приходилась на интервал $22 – 26^\circ C$, что является наибольшей концентрацией наблюдений.

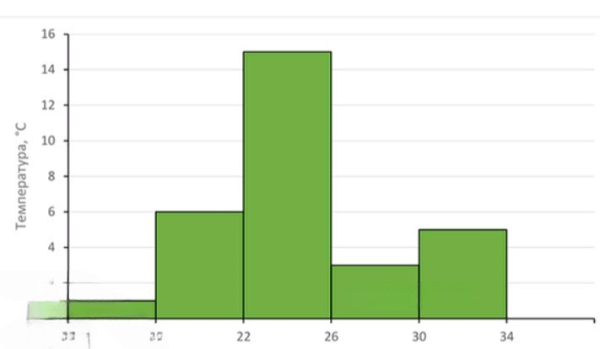
2) Гистограмма частот для 2010 года:

Гистограмма представляет собой графическое изображение распределения данных по интервалам. По оси абсцисс откладываются интервалы температур, а по оси ординат — частоты (абсолютные или относительные). Для каждого интервала строится прямоугольник: основание прямоугольника соответствует ширине интервала (в данном случае все интервалы равны по ширине и составляют $4^\circ C$), а высота — частоте.

Для интервала $14 – 18^\circ C$ высота прямоугольника равна 1 (или относительной частоте 0,033), для интервала $18 – 22^\circ C$ — 6 (или 0,2), для интервала $22 – 26^\circ C$ — 15 (или 0,5), для интервала $26 – 30^\circ C$ — 3 (или 0,1), для интервала $30 – 34^\circ C$ — 5 (или 0,167).

Построив гистограмму, мы наглядно увидим, что наиболее высокий прямоугольник приходится на интервал $22 – 26^\circ C$, что подтверждает максимальную частоту в 15 дней. Более низкие прямоугольники будут соответствовать остальным интервалам, показывая постепенное уменьшение числа дней.

Таким образом, гистограмма является удобным способом наглядного представления распределения температурных данных и позволяет легко сравнить частоты наблюдений по различным интервалам.