ГДЗ по Алгебре 9 Класс Это Надо Уметь Глава 5 Номер 1 Дорофеев, Суворова — Подробные Ответы

Используя диаграмму на рисунке 5.5, выполните задания:
а) построЙте таблицу для количества квартир, если всего в городе 1 млн квартир;
б) постройте соответствующий полигон количества квартир;
в) определите по таблице среднее количество комнат в квартире.

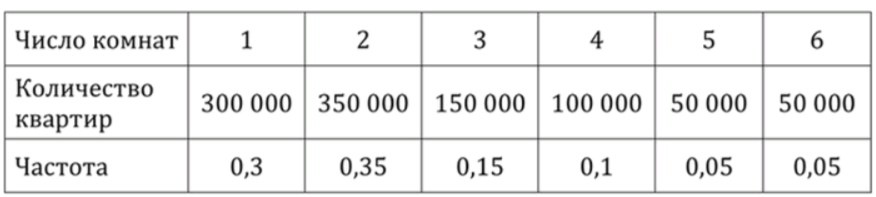
а) Таблица количества комнат, если всего в городе 1 млн квартир:

$S = 1\,000\,000$;

$N_1 = 1\,000\,000 \cdot 0,3 = 300\,000$;

$N_2 = 1\,000\,000 \cdot 0,35 = 350\,000$;

$N_3 = 1\,000\,000 \cdot 0,15 = 150\,000$;

$N_4 = 1\,000\,000 \cdot 0,1 = 100\,000$;

$N_5 = N_6 = 1\,000\,000 \cdot 0,05 = 50\,000$;

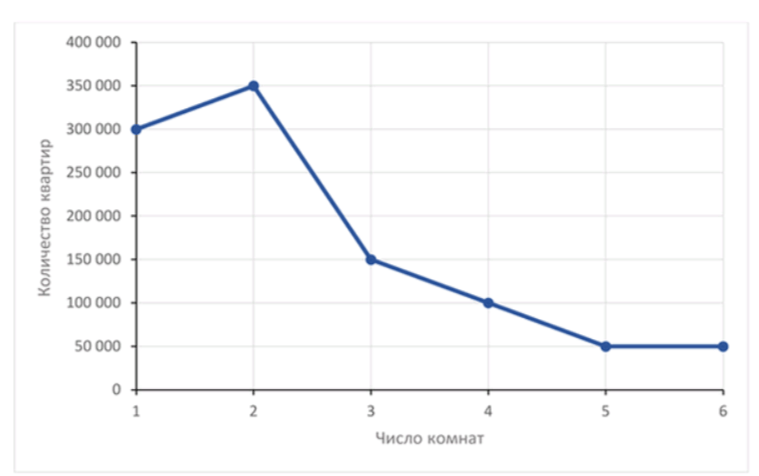
б) Полигон количества квартир:

в) Среднее количество комнат в квартире:

$\overline{x} = \frac{(1 \cdot 0,3 + 2 \cdot 0,35 + 3 \cdot 0,15 + 4 \cdot 0,1 + 5 \cdot 0,05 + 6 \cdot 0,05) \cdot 10^6}{1 \cdot 10^6} =$

$= 0,3 + 0,7 + 0,45 + 0,4 + 0,25 + 0,3 = 2,4 \approx 2$;

а) Таблица количества комнат, если всего в городе 1 млн квартир:

В таблице отражено распределение квартир по числу комнат. В городе всего $S = 1\,000\,000$ квартир. Указанные частоты показывают долю квартир с определённым количеством комнат. Например, частота $0,3$ означает, что 30% всех квартир — это однокомнатные квартиры.

б) Проверим вычисления количества квартир для каждой категории, используя соотношение $N_i = S \cdot f_i$, где $f_i$ — частота для категории, а $S$ — общее число квартир.

Для одной комнаты:
$N_1 = 1\,000\,000 \cdot 0,3 = 300\,000$. Это значит, что в городе 300 тысяч квартир состоят из одной комнаты.

Для двух комнат:
$N_2 = 1\,000\,000 \cdot 0,35 = 350\,000$. Это значит, что доля двухкомнатных квартир составляет 35%, то есть таких квартир 350 тысяч.

Для трёх комнат:
$N_3 = 1\,000\,000 \cdot 0,15 = 150\,000$. Таким образом, 15% квартир в городе — это трёхкомнатные квартиры, и их число составляет 150 тысяч.

Для четырёх комнат:
$N_4 = 1\,000\,000 \cdot 0,1 = 100\,000$. Значит, четырёхкомнатные квартиры составляют 10% всех квартир, то есть 100 тысяч.

Для пяти и шести комнат:
$N_5 = N_6 = 1\,000\,000 \cdot 0,05 = 50\,000$. Это означает, что как пятикомнатные, так и шестикомнатные квартиры составляют по 5% от общего количества, то есть по 50 тысяч квартир каждой категории.

Итоговое распределение: 300 000 однокомнатных, 350 000 двухкомнатных, 150 000 трёхкомнатных, 100 000 четырёхкомнатных, 50 000 пятикомнатных и 50 000 шестикомнатных.

в) Среднее количество комнат в квартире определяется по формуле среднего арифметического взвешенного:

$\overline{x} = \frac{\sum (x_i \cdot f_i \cdot S)}{S}$.

Так как $S$ сокращается, то формула упрощается до:
$\overline{x} = \sum (x_i \cdot f_i)$, где $x_i$ — количество комнат, $f_i$ — частота для данной категории.

Подставим данные:
$\overline{x} = 1 \cdot 0,3 + 2 \cdot 0,35 + 3 \cdot 0,15 + 4 \cdot 0,1 + 5 \cdot 0,05 + 6 \cdot 0,05$.

Вычислим каждое слагаемое:
$1 \cdot 0,3 = 0,3$,
$2 \cdot 0,35 = 0,7$,
$3 \cdot 0,15 = 0,45$,
$4 \cdot 0,1 = 0,4$,
$5 \cdot 0,05 = 0,25$,
$6 \cdot 0,05 = 0,3$.

Сложим:
$\overline{x} = 0,3 + 0,7 + 0,45 + 0,4 + 0,25 + 0,3 = 2,4$.

Таким образом, среднее количество комнат в квартире составляет $\overline{x} = 2,4$.

Так как количество комнат должно выражаться целым числом, округляем до ближайшего целого: приблизительно 2 комнаты.