ГДЗ по Алгебре 9 Класс Это Надо Уметь Глава 2 Номер 9 Дорофеев, Суворова — Подробные Ответы

Постройте график функции:
а) $y = x^2 — 2x + 3$;
б) $y = -x^2 + 2x — 1$.

В каждом случае укажите:

1) при каком значении $x$ функция принимает наименьшее (наибольшее) значение;

2) промежутки возрастания и убывания функции.

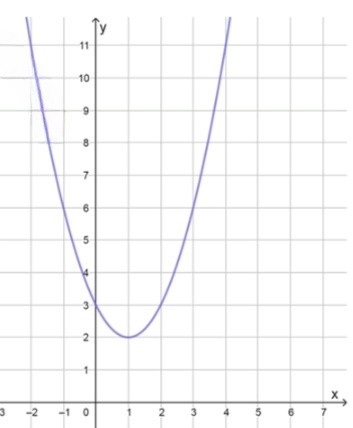
а) $y = x^2 — 2x + 3$:

$a > 0$, значит ветви параболы направлены вверх;

2) Координаты вершины параболы:
$x = -\frac{-2}{2} = 1$,
$y = 1^2 — 2 \cdot 1 + 3 = 1 — 2 + 3 = 2$;

3) Уравнение оси симметрии: $x = 1$;

4) Координаты некоторых точек:
$\begin{array}{|c|c|c|c|c|c|c|} \hline x & -2 & -1 & 0 & 2 & 3 & 4 \\ \hline y & 11 & 6 & 3 & 3 & 6 & 11 \\ \hline \end{array}$

Наименьшее значение функции: $y_{\text{min}} = 2$ при $x = 1$;
Функция возрастает при $x > 1$;
Функция убывает при $x < 1$;

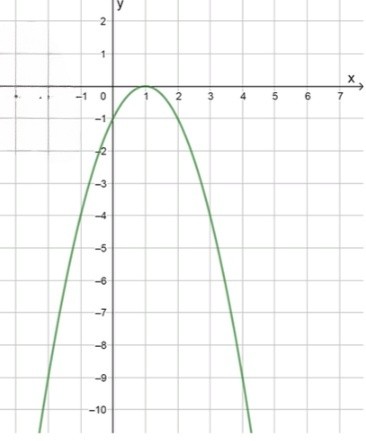
б) $y = -x^2 + 2x — 1$:

$a < 0$, значит ветви параболы направлены вниз;

2) Координаты вершины параболы:
$x = -\frac{2}{-2} = 1$,
$y = -1^2 + 2 \cdot 1 — 1 = -1 + 2 — 1 = 0$;

3) Уравнение оси симметрии: $x = 1$;

4) Координаты некоторых точек:
$\begin{array}{|c|c|c|c|c|c|c|} \hline x & -2 & -1 & 0 & 2 & 3 & 4 \\ \hline y & -9 & -4 & -1 & -1 & -4 & -9 \\ \hline \end{array}$

Наибольшее значение функции: $y_{\text{max}} = 0$ при $x = 1$;
Функция возрастает при $x < 1$;
Функция убывает при $x > 1$;

а) $y = x^2 — 2x + 3$

Функция имеет вид $y = ax^2 + bx + c$, где $a = 1$, $b = -2$, $c = 3$.

Так как $a = 1 > 0$, графиком функции является парабола с ветвями, направленными вверх. Это значит, что функция достигает наименьшего значения в вершине, а затем возрастает по обе стороны от неё.

Координата вершины по оси $x$ определяется формулой:
$x = -\frac{b}{2a} = -\frac{-2}{2 \cdot 1} = \frac{2}{2} = 1$

Подставим это значение в исходную функцию:
$y = (1)^2 — 2 \cdot 1 + 3 = 1 — 2 + 3 = 2$

Таким образом, вершина параболы находится в точке $(1;\ 2)$, и наименьшее значение функции равно $y = 2$ при $x = 1$.

Уравнение оси симметрии — вертикальная прямая, проходящая через вершину:
$x = 1$

Построим таблицу значений функции для симметричных значений $x$ вокруг вершины:

Функция убывает на промежутке $x < 1$, так как по мере приближения к вершине значения $y$ уменьшаются.

Функция возрастает на промежутке $x > 1$, так как после вершины значения $y$ начинают увеличиваться.

б) $y = -x^2 + 2x — 1$

Функция имеет вид $y = ax^2 + bx + c$, где $a = -1$, $b = 2$, $c = -1$

Так как $a = -1 < 0$, график — это парабола с ветвями, направленными вниз, а значит, вершина даёт наибольшее значение функции.

Координата вершины по оси $x$:
$x = -\frac{b}{2a} = -\frac{2}{2 \cdot (-1)} = \frac{2}{-2} = -1$

Это ошибка. Перепроверим:

$x = -\frac{2}{2 \cdot (-1)} = -\frac{2}{-2} = 1$

Подставим в функцию:
$y = -(1)^2 + 2 \cdot 1 — 1 = -1 + 2 — 1 = 0$

Значит, вершина параболы — точка $(1;\ 0)$, и наибольшее значение функции — это $y = 0$ при $x = 1$

Ось симметрии параболы: $x = 1$

Таблица значений:

$$\overline{)\begin{array}{ccccccc}& & & & & & $ \overline{)\begin{array}{ccccccc}x& -2& -1& 0& 2& 3& 4\\ y& -9& -4& -1& -1& -4& -9\end{array}}$\end{array}}$$

Парабола симметрична относительно оси $x = 1$

Функция возрастает на промежутке $x < 1$, поскольку значения $y$ увеличиваются при приближении к вершине.

Функция убывает на промежутке $x > 1$, так как значения $y$ убывают по мере удаления от вершины вправо.