ГДЗ по Алгебре 9 Класс Это Надо Уметь Глава 2 Номер 3 Дорофеев, Суворова — Подробные Ответы

Постройте график функции:
а) $y = \frac{1}{2}x^2$;
б) $y = -x^2$.

В каждом случае укажите промежутки возрастания и убывания функции.

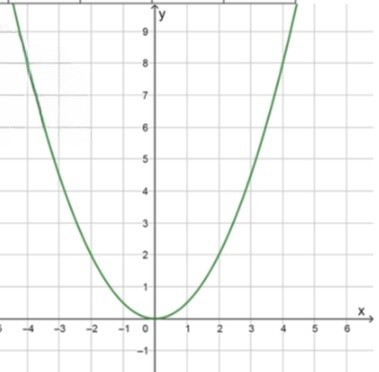
а) $y = \frac{1}{2}x^2$:

• $a > 0$, значит ветви параболы направлены вверх;
• Вершина параболы находится в точке $(0;\ 0)$;
• Уравнение оси симметрии: $x = 0$;
• Координаты некоторых точек:
  $\begin{array}{|c|c|c|c|c|} \hline x & -4 & -2 & 2 & 4 \\ \hline y & 8 & 2 & 2 & 8 \\ \hline \end{array}$

Функция возрастает при $x > 0$;
Функция убывает при $x < 0$;

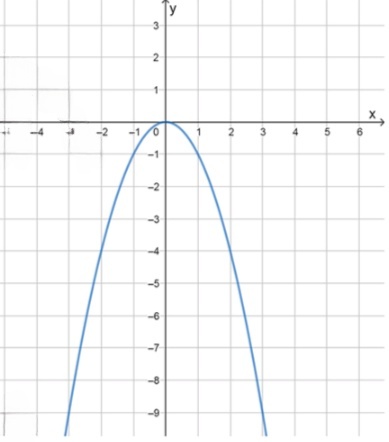
б) $y = -x^2$:

• $a < 0$, значит ветви параболы направлены вниз;
• Вершина параболы находится в точке $(0;\ 0)$;
• Уравнение оси симметрии: $x = 0$;
• Координаты некоторых точек:
  $\begin{array}{|c|c|c|c|c|c|} \hline x & -3 & -2 & -1 & 1 & 2 & 3 \\ \hline y & -9 & -4 & -1 & -1 & -4 & -9 \\ \hline \end{array}$

Функция возрастает при $x < 0$;
Функция убывает при $x > 0$.

а) $y = \frac{1}{2}x^2$:

Это квадратичная функция, имеющая вид $y = ax^2$, где $a = \frac{1}{2} > 0$.

— Поскольку коэффициент $a$ положителен, график функции представляет собой параболу с ветвями, направленными вверх. Это означает, что по мере удаления от вершины влево или вправо значения функции возрастают.

— Вершина параболы — это точка минимума, так как парабола открыта вверх. Формула вершины для функции вида $y = ax^2$ — это точка $(0;\ 0)$, поскольку $x = 0$, и $y = \frac{1}{2} \cdot 0^2 = 0$.

— Ось симметрии проходит через вершину, а значит, уравнение оси симметрии: $x = 0$. Это вертикальная прямая, которая делит параболу на две симметричные части: левая ветвь и правая ветвь зеркальны относительно этой прямой.

— Значения функции на симметричных точках равны, например:

$$\begin{array}{|c|c|c|c|c|} \hline x & -4 & -2 & 2 & 4 \\ \hline y & \frac{1}{2} \cdot 16 = 8 & \frac{1}{2} \cdot 4 = 2 & \frac{1}{2} \cdot 4 = 2 & \frac{1}{2} \cdot 16 = 8 \\ \hline \end{array}$$

— Функция убывает на интервале $x < 0$, поскольку при движении слева направо к вершине значения $y$ уменьшаются.

— Функция возрастает на интервале $x > 0$, поскольку при дальнейшем движении вправо от вершины значения $y$ снова увеличиваются.

То есть:

• убывание: при $x < 0$;
• возрастание: при $x > 0$.

График представляет собой симметричную параболу с вершиной в начале координат и плавным подъёмом/спадом, зависящим от коэффициента $a = \frac{1}{2}$, который делает её широкой (медленно растущей).

б) $y = -x^2$:

Это тоже квадратичная функция, но теперь $a = -1$, то есть отрицательный коэффициент при $x^2$.

— Раз $a < 0$, то ветви параболы направлены вниз. Это означает, что вершина будет точкой максимума, и по мере удаления от неё значения функции убывают.

— Вершина функции находится в точке $(0;\ 0)$, так как подставляя $x = 0$, получаем $y = -0^2 = 0$.

— Ось симметрии — вертикальная прямая, проходящая через вершину: $x = 0$. График симметричен относительно этой прямой.

— Координаты некоторых характерных точек:

$$\begin{array}{|c|c|c|c|c|c|} \hline x & -3 & -2 & -1 & 1 & 2 & 3 \\ \hline y & -9 & -4 & -1 & -1 & -4 & -9 \\ \hline \end{array}$$

— Функция возрастает на интервале $x < 0$, так как при движении к вершине слева направо значения $y$ увеличиваются.

— Функция убывает на интервале $x > 0$, так как при дальнейшем движении вправо от вершины значения $y$ уменьшаются.

То есть:

• возрастание: при $x < 0$;
• убывание: при $x > 0$.

График — это узкая, симметричная парабола с вершиной в начале координат, направленная вниз. Коэффициент $a = -1$ делает её стандартной по ширине и показывает, что значения функции будут убывать быстрее, чем у параболы $y = \frac{1}{2}x^2$.