
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Это Надо Уметь Глава 2 Номер 10 Дорофеев, Суворова — Подробные Ответы
Решите неравенство:
а) ;
б) ;
в) ;
г) ;
д) ;
е) .
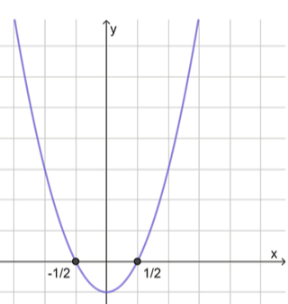
а) :
, значит ветви направлены вверх;
2) Нули функции:
3) Схематический рисунок:
Ответ: .
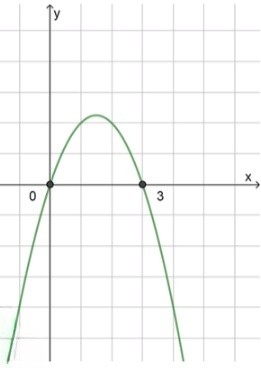
б) :
, значит ветви направлены вниз;
2) Нули функции:
3) Схематический рисунок:
Ответ: .
в) :
, значит ветви направлены вверх;
2) Нули функции:
3) Схематический рисунок:
Ответ: .
г) :
, значит ветви направлены вверх;
2) Нули функции:
3) Схематический рисунок:
Ответ: .
д) :
, значит ветви направлены вверх;
2) Нули функции:
3) Схематический рисунок:
Ответ: .
е) :
, значит ветви направлены вниз;
2) Нули функции:
3) Схематический рисунок:
Ответ: .
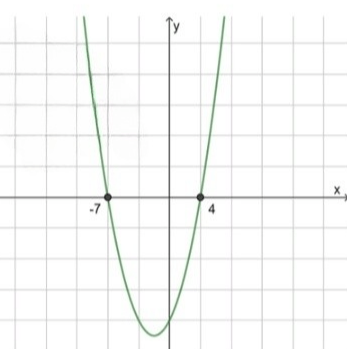
а) :
Коэффициент при равен . Поскольку , парабола имеет ветви, направленные вверх, то есть график открывается вверх.
Найдём корни квадратного уравнения по формуле корней:
Дискриминант:
Корни уравнения:
Поскольку ветви направлены вверх, и нам нужно найти, где квадратичное выражение меньше нуля, т.е. , это происходит между корнями параболы, т.е. на интервале, где график лежит ниже оси абсцисс.
Значит, решением будет промежуток:
Графически: парабола пересекает ось в точках и , а ниже оси она находится между этими точками.
Ответ:
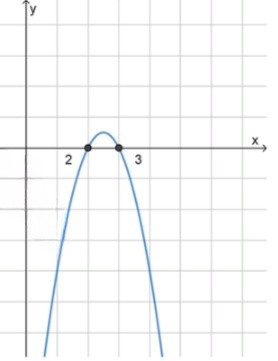
б) :
Коэффициент при : , следовательно, ветви параболы направлены вниз, то есть график открывается вниз.
Решим уравнение , чтобы найти точки пересечения графика с осью .
Применим формулу дискриминанта:
Найдём корни уравнения:
Порядок: ,
Ветви направлены вниз, следовательно, парабола лежит выше оси между корнями, и ниже или на оси вне корней. Так как знак неравенства , нас интересуют области, где значение выражения меньше либо равно нулю, то есть внешние области параболы и точки пересечения.
Таким образом,
Ответ:
в) :
Коэффициент , ветви параболы направлены вверх.
Решим уравнение для нахождения возможных точек пересечения с осью :
Переносим константу:
Делим обе части на 2:
Так как квадрат действительного числа не может быть отрицательным, уравнение не имеет действительных решений.
Следовательно, график параболы не пересекает ось абсцисс и находится всё время выше неё, потому что .
Неравенство строгое: , и значение функции всегда положительное, так как нет корней и ветви вверх.
Ответ:
г) :
, ветви параболы направлены вверх.
Найдём дискриминант:
Дискриминант отрицательный, значит, уравнение не имеет действительных корней. График не пересекает ось .
Поскольку , график всегда выше оси , значение выражения всегда положительное, а значит для всех . Но в неравенстве стоит знак , а такого , при котором выражение , не существует.
Ответ:
д) :
, значит, ветви направлены вверх.
Перепишем неравенство в виде уравнения для нахождения граничных точек:
Извлекаем корень:
Так как , ветви вверх. Значения функции меньше между корнями и больше или равно вне корней.
Знак неравенства , нас интересуют значения от и выше, то есть всё вне интервала
Ответ:
е) :
Перенесём всё в одну сторону:
Приведём к каноническому виду:
Коэффициент , значит, ветви направлены вниз.
Найдём корни уравнения:
Вынесем за скобку:
Приравниваем каждый множитель к нулю:
,
Так как ветви вниз, парабола между корнями лежит над осью . А нас интересует область, где выражение , то есть включая точки пересечения и участок, где график выше оси .
Ответ:




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!