
Учебник по Алгебре для 8-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 8 Класс Номер 897 Дорофеев, Суворова — Подробные Ответы
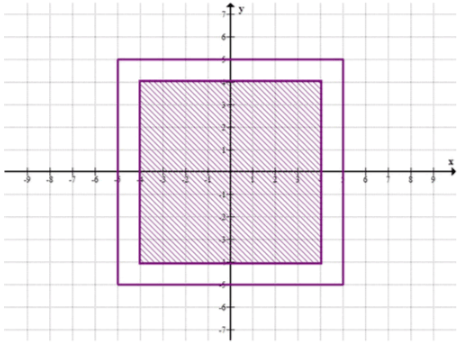
Фигура Ф задана на координатной плоскости следующими условиями: |x| < =5 и |y| < =5. Известно, что центр квадрата со сторонами, параллельными осям координат, принадлежат фигуре Ф. Сторона квадрата равна 2. Какова вероятность того, что квадрат целиком содержится в фигуре Ф
Исход благоприятен, если центр лежит в квадрате со стороной 8 и с центром в начале координат.
Площадь заштрихованного квадрата равна 64.
Вероятность равна .
Ответ: 0,64.
Исход благоприятен, если центр лежит в квадрате со стороной 8 и с центром в начале координат.
Для начала, рассмотрим квадрат, который имеет сторону равную 8. Площадь этого квадрата вычисляется по формуле площади квадрата:
где — длина стороны квадрата. Подставляем значение стороны квадрата :
Таким образом, площадь квадрата, в котором центр находится в начале координат, равна 64.
Теперь, для нахождения вероятности, нужно определить отношение площади заштрихованного квадрата к общей площади, которая составляет 100. Площадь заштрихованного квадрата — это та область, в которой возможен благоприятный исход. Следовательно, вероятность попадания в эту область будет равна отношению площади заштрихованного квадрата к общей площади. Площадь заштрихованного квадрата равна 64, а общая площадь — 100. Тогда вероятность можно выразить как:
Таким образом, вероятность благоприятного исхода составляет .
Ответ: 0,64.




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!