
Учебник по Алгебре для 8-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 8 Класс Номер 756 Дорофеев, Суворова — Подробные Ответы
;
;
;
;
;
.
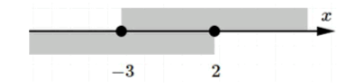
а) — отрезок ;
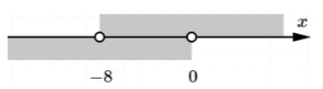
б) — интервал ;
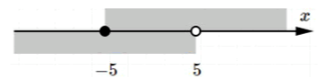
в) — полуинтервал ;
г) — замкнутый луч ;
д) — замкнутый луч ;
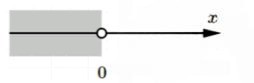
е) — открытый луч .
- — отрезок ;
Для того чтобы понять, что это за отрезок, представим себе на числовой оси два числа: и . Указание на нестрогие неравенства (включая эти числа) означает, что может принимать значения от до , включая оба этих числа. Это и есть отрезок от до , который включает в себя все числа между ними, а также сами концы отрезка и . Таким образом, это область значений , в которой может быть любым числом, лежащим на этом отрезке.
- — интервал ;
Здесь мы имеем строгие неравенства, что означает, что может быть любым числом, лежащим между и , но самих чисел и в интервале нет. Мы называем этот интервал открытым на обоих концах, так как значения и не включаются. Это означает, что может быть очень близким к или , но не равным этим числам.
- — полуинтервал ;
Здесь указано, что может принимать значения от до , но не включается в этот полуинтервал. Он включает в себя все числа от до , где включается, а нет. Это полуинтервал, который начинается с и продолжается до , не включая , но включает все числа между и .
- — замкнутый луч ;
Здесь мы имеем нестрогое неравенство , что означает, что может быть равно или любым числом больше . Это замкнутый луч, который начинается с числа и продолжается вправо бесконечно. Обратите внимание, что в этом случае число включается в область, так как используется нестрогое неравенство. Это замкнутый луч, который включает все числа больше или равные .
- — замкнутый луч ;
Это нестрогое неравенство означает, что может быть любым числом, меньшим или равным . Это замкнутый луч, который идет влево от и включает все числа, меньшие или равные . также включается в область, так как используется нестрогое неравенство. Это замкнутый луч, который продолжается влево от , включая все числа до , но не ограничиваясь этим числом.
- — открытый луч .
Это нестрогое неравенство означает, что может быть любым числом, которое меньше нуля. Это открытый луч, который начинается от нуля и идет влево бесконечно. Обратите внимание, что здесь не включается, потому что используется строгое неравенство. Это открытый луч, который включает все отрицательные числа, но не включает саму точку .






Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!