ГДЗ по Алгебре 8 Класс Номер 701 Дорофеев, Суворова — Подробные Ответы

а) $x^2 + y^2 \leq 1$

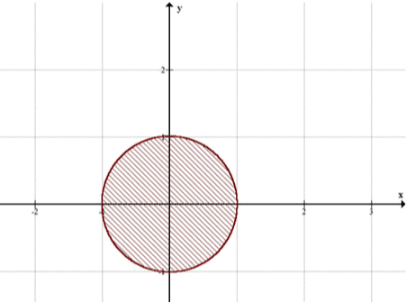
→ круг, центр которого в начале координат, а радиус равен 1.

б) $x^2 + y^2 \geq 9$

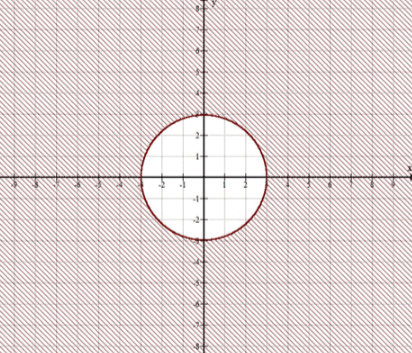
→ часть плоскости, которая расположена вне круга с центром в начале координат и радиусом, равным 3.

в)

$$\begin{cases} x^2 + y^2 \geq 1 \\ x^2 + y^2 \leq 9 \end{cases}$$

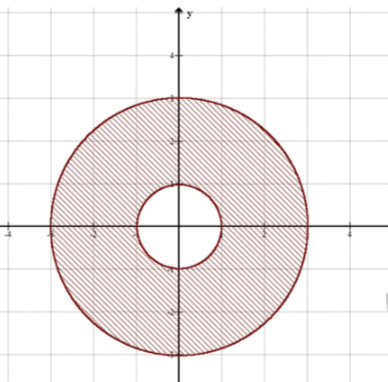
→ кольцо, которое ограничено двумя концентрическими окружностями, центры которых в начале координат, а радиусы равны 1 и 3.

а) $x^2 + y^2 \leq 1$

Уравнение $x^2 + y^2 = 1$ задаёт окружность с центром в начале координат и радиусом 1.

Неравенство $x^2 + y^2 \leq 1$ означает, что рассматриваются все точки, которые лежат внутри этой окружности, включая её границу.

Таким образом, множество точек, удовлетворяющих неравенству $x^2 + y^2 \leq 1$, это весь круг, который имеет центр в точке $(0, 0)$ и радиус 1.

Ответ:
Это множество точек внутри и на окружности радиусом 1 с центром в начале координат.

б) $x^2 + y^2 \geq 9$

Уравнение $x^2 + y^2 = 9$ представляет собой окружность с центром в начале координат и радиусом 3.

Неравенство $x^2 + y^2 \geq 9$ означает, что рассматриваются все точки, которые лежат вне этой окружности, включая её границу.

Таким образом, множество точек, удовлетворяющих неравенству $x^2 + y^2 \geq 9$, это внешняя область вокруг окружности с радиусом 3, включая саму окружность.

Ответ:
Это множество точек, расположенных вне окружности радиусом 3 с центром в начале координат.

в)

$$\begin{cases} x^2 + y^2 \geq 1 \\ x^2 + y^2 \leq 9 \end{cases}$$

Уравнение $x^2 + y^2 = 1$ задаёт окружность радиусом 1, а уравнение $x^2 + y^2 = 9$ задаёт окружность радиусом 3.

Неравенство $x^2 + y^2 \geq 1$ определяет область, которая находится вне окружности радиусом 1.

Неравенство $x^2 + y^2 \leq 9$ определяет область, которая находится внутри окружности радиусом 3.

Совмещение этих двух условий даёт кольцевую область между двумя окружностями: одна с радиусом 1 (включена), а другая с радиусом 3 (включена).

Ответ:
Это множество точек, которые находятся между двумя концентрическими окружностями с радиусами 1 и 3, центры которых находятся в начале координат.