
Учебник по Алгебре для 8-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 8 Класс Номер 642 Дорофеев, Суворова — Подробные Ответы
Объясните, почему данная система не имеет решений или имеет бесчисленное множество решений (в этом случае приведите примеры решений):
а)
б)
в)
г)
д)
е)
а)
Решение:
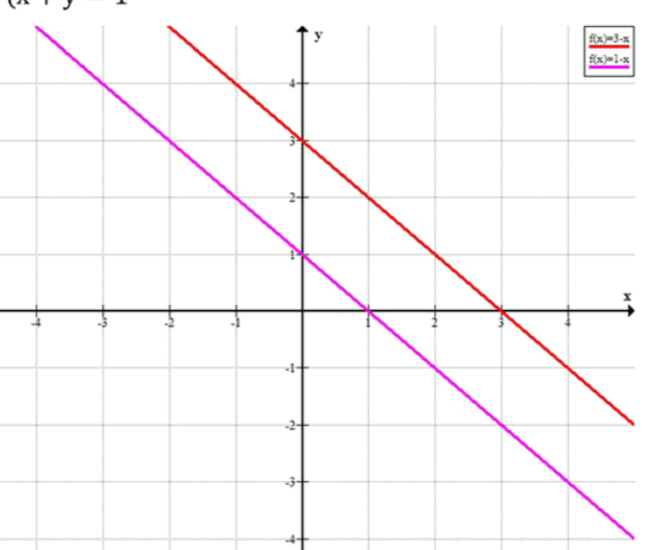
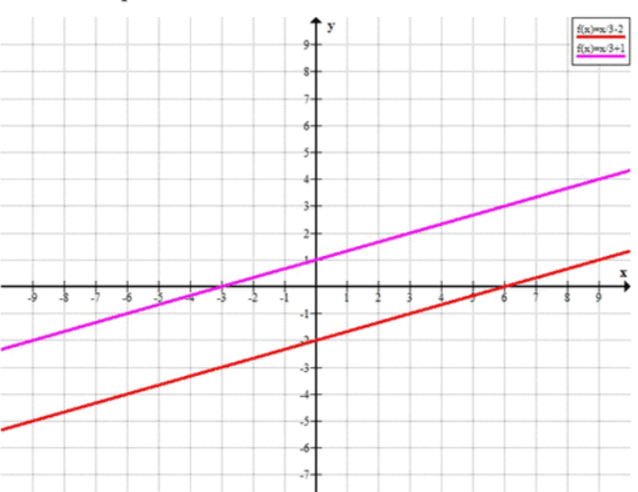
Оба уравнения имеют одинаковые левые части, но разные правые части. Это означает, что прямые, соответствующие этим уравнениям, параллельны и не пересекаются.
- Графически: Обе прямые имеют наклон (коэффициент ), но разные свободные члены ( и ). Они никогда не пересекаются.
Ответ: Система не имеет решений.
б)
Решение:
Оба уравнения имеют одинаковые левые части, но разные правые части. Это означает, что прямые, соответствующие этим уравнениям, параллельны и не пересекаются.
- Графически: Обе прямые имеют наклон (коэффициент ), но разные свободные члены ( и ). Они никогда не пересекаются.
Ответ: Система не имеет решений.
в)
Решение:
Второе уравнение можно разделить на :
Теперь система выглядит так:
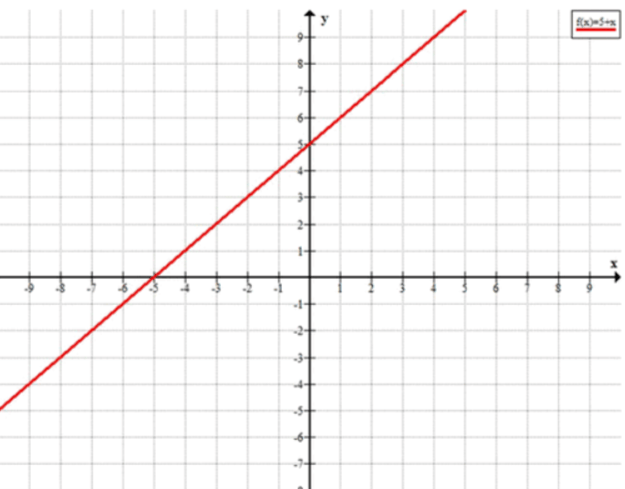
Это одно и то же уравнение, записанное дважды. Значит, обе прямые совпадают, и система имеет бесконечно много решений.
- Графически: Обе прямые совпадают, так как они представляют одну и ту же линию с уравнением .
Ответ: Система имеет бесконечно много решений.
г)
Решение:
Второе уравнение можно разделить на :
Теперь система выглядит так:
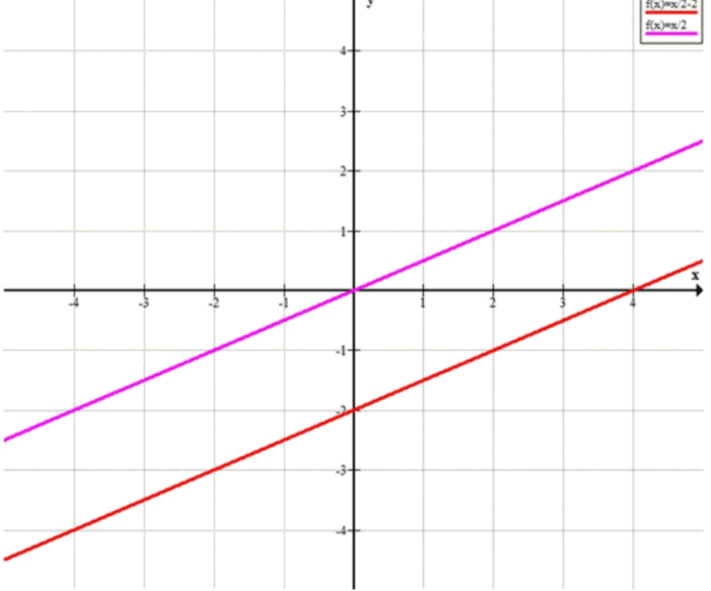
Оба уравнения имеют одинаковые левые части, но разные правые части. Это означает, что прямые, соответствующие этим уравнениям, параллельны и не пересекаются.
- Графически: Обе прямые имеют наклон (коэффициент ), но разные свободные члены ( и ). Они никогда не пересекаются.
Ответ: Система не имеет решений.
д)
Решение:
Второе уравнение можно разделить на :
Теперь система выглядит так:
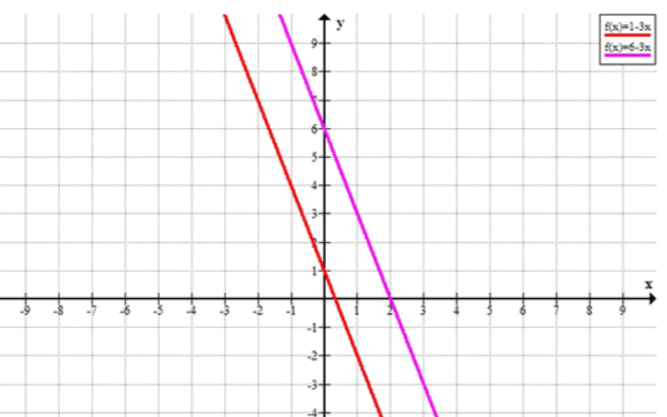
Оба уравнения имеют одинаковые левые части, но разные правые части. Это означает, что прямые, соответствующие этим уравнениям, параллельны и не пересекаются.
- Графически: Обе прямые имеют наклон (коэффициент ), но разные свободные члены ( и ). Они никогда не пересекаются.
Ответ: Система не имеет решений.
е)
Решение:
Умножаем второе уравнение на :
Теперь система выглядит так:
Первое уравнение можно разделить на :
Теперь система выглядит так:
Это одно и то же уравнение, записанное дважды. Значит, обе прямые совпадают, и система имеет бесконечно много решений.
- Графически: Обе прямые совпадают, так как они представляют одну и ту же линию с уравнением .
Ответ: Система имеет бесконечно много решений.
а)
Решение:
Оба уравнения имеют одинаковые левые части, но разные правые части. Это означает, что прямые, соответствующие этим уравнениям, параллельны и не пересекаются.
- Графически: Обе прямые имеют наклон (коэффициент ), но разные свободные члены ( и ). Они никогда не пересекаются.
Ответ: Система не имеет решений.
б)
Решение:
Оба уравнения имеют одинаковые левые части, но разные правые части. Это означает, что прямые, соответствующие этим уравнениям, параллельны и не пересекаются.
- Графически: Обе прямые имеют наклон (коэффициент ), но разные свободные члены ( и ). Они никогда не пересекаются.
Ответ: Система не имеет решений.
в)
Решение:
Второе уравнение можно разделить на :
Теперь система выглядит так:
Это одно и то же уравнение, записанное дважды. Значит, обе прямые совпадают, и система имеет бесконечно много решений.
- Графически: Обе прямые совпадают, так как они представляют одну и ту же линию с уравнением .
Ответ: Система имеет бесконечно много решений.
г)
Решение:
Второе уравнение можно разделить на :
Теперь система выглядит так:
Оба уравнения имеют одинаковые левые части, но разные правые части. Это означает, что прямые, соответствующие этим уравнениям, параллельны и не пересекаются.
- Графически: Обе прямые имеют наклон (коэффициент ), но разные свободные члены ( и ). Они никогда не пересекаются.
Ответ: Система не имеет решений.
д)
Решение:
Второе уравнение можно разделить на :
Теперь система выглядит так:
Оба уравнения имеют одинаковые левые части, но разные правые части. Это означает, что прямые, соответствующие этим уравнениям, параллельны и не пересекаются.
- Графически: Обе прямые имеют наклон (коэффициент ), но разные свободные члены ( и ). Они никогда не пересекаются.
Ответ: Система не имеет решений.
е)
Решение:
Умножаем второе уравнение на :
Теперь система выглядит так:
Первое уравнение можно разделить на :
Теперь система выглядит так:
Это одно и то же уравнение, записанное дважды. Значит, обе прямые совпадают, и система имеет бесконечно много решений.
- Графически: Обе прямые совпадают, так как они представляют одну и ту же линию с уравнением .
Ответ: Система имеет бесконечно много решений.




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!