ГДЗ по Алгебре 8 Класс Номер 632 Дорофеев, Суворова — Подробные Ответы

Постройте график уравнения:
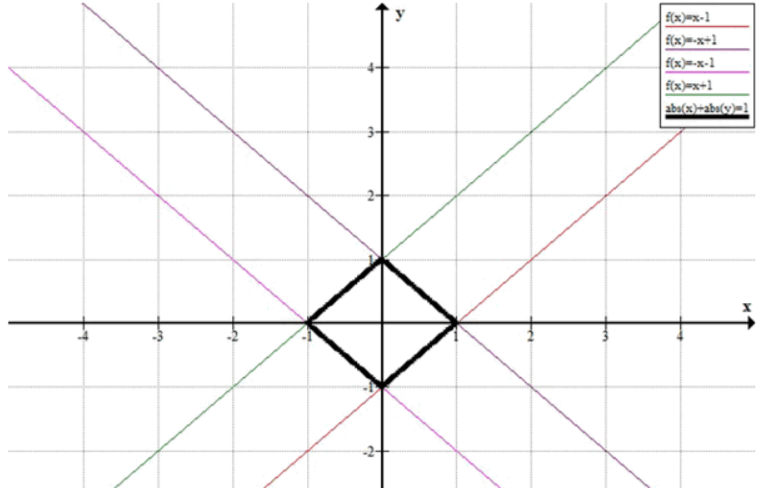
а) |x|+|y|=1;
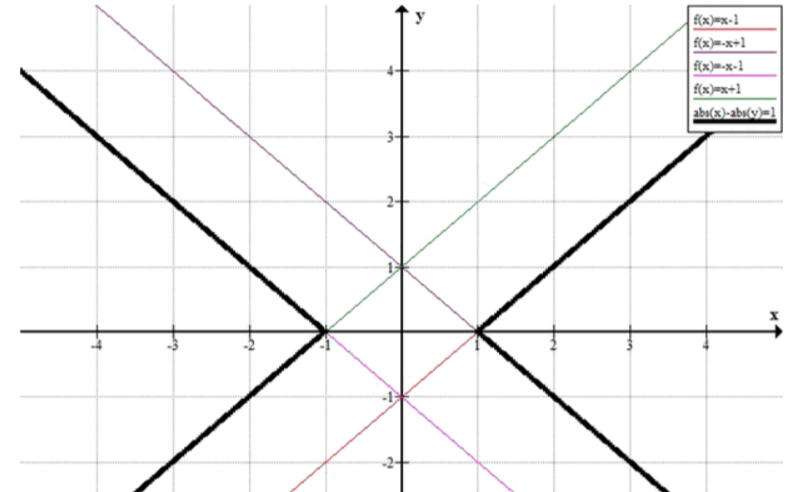
б) |x|-|y|=1.

a) $\mathrm{\mid }x\mathrm{\mid }+\mathrm{\mid }y\mathrm{\mid }=1$

• Если $x\ge 0$ и $y\ge 0$, то $x+y=1\to y=-x+1$;
• Если $x\ge 0$ и $y\le 0$, то $x-y=1\to y=x-1$;
• Если $x\le 0$ и $y\ge 0$, то $-x+y=1\to y=x+1$;
• Если$x\le 0$ и $y\le 0$, то$-x-y=1\to y=-x-1$.

График:

б) $\mathrm{\mid }x\mathrm{\mid }-\mathrm{\mid }y\mathrm{\mid }=1$

• Если $x\ge 0$ и $y\ge 0$, то $x-y=1\to y=x-1$;
• Если $x\ge 0$ и $y\le 0$, то $x+y=1\to y=-x+1$;
• Если $x\le 0$ и $y\ge 0$, то $-x-y=1\to y=-x-1$;
• Если $x\le 0$ и $y\le 0$, то $-x+y=1\to y=x+1$.

График:

a) $\mathrm{\mid }x\mathrm{\mid }+\mathrm{\mid }y\mathrm{\mid }=1$

Это уравнение описывает геометрическую фигуру, которая является ромбом, расположенным с центром в начале координат. Для определения вида этой фигуры и её составляющих разберем все возможные случаи для значений $x$ и $y$, учитывая, что модули чисел могут влиять на знак каждого из слагаемых.

1. Рассмотрим случай $x\ge 0$ и $y\ge 0$:

В этом случае модули можно опустить, так как оба значения $x$ и $y$ не отрицательны. Уравнение $\mathrm{\mid }x\mathrm{\mid }+\mathrm{\mid }y\mathrm{\mid }=1$ превращается в:

$$x+y=1.$$

Решим его относительно $y$:

$$y=1-x\mathrm{.}$$

Это уравнение прямой с угловым коэффициентом $-1$, которая проходит через точку $(0,1)$ на оси $y$ и точку $(1,0)$ на оси $x$.

2. Рассмотрим случай $x\ge 0$ и $y\le 0$:

Здесь $x$ остаётся положительным, а $y$ отрицательным, поэтому модуль $\mathrm{\mid }y\mathrm{\mid }=-y$. Уравнение $\mathrm{\mid }x\mathrm{\mid }+\mathrm{\mid }y\mathrm{\mid }=1$ превращается в:

$$x-y=1.$$

Решим его относительно $y$:

$$y=x-1.$$

Это уравнение прямой, которая пересекает ось $y$ в точке $(0,-1)$ и ось $x$ в точке $(1,0)$, но с угловым коэффициентом $1$.

3. Рассмотрим случай $x\le 0$ и $y\ge 0$:

Здесь $x$ отрицателен, а $y$ положителен, поэтому $\mathrm{\mid }x\mathrm{\mid }=-x$ и $\mathrm{\mid }y\mathrm{\mid }=y$. Уравнение $\mathrm{\mid }x\mathrm{\mid }+\mathrm{\mid }y\mathrm{\mid }=1$ превращается в:

$$-x+y=1.$$

Решим его относительно $y$:

$$y=x+1.$$

Это уравнение прямой, которая пересекает ось $y$ в точке $(0,1)$ и ось $x$ в точке $(-1,0)$, с угловым коэффициентом $1$.

4. Рассмотрим случай $x\le 0$ и $y\le 0$:

Здесь оба значения $x$ и $y$ отрицательны, поэтому $\mathrm{\mid }x\mathrm{\mid }=-x$ и $\mathrm{\mid }y\mathrm{\mid }=-y$. Уравнение $\mathrm{\mid }x\mathrm{\mid }+\mathrm{\mid }y\mathrm{\mid }=1$ превращается в:

$$-x-y=1.$$

Решим его относительно $y$:

$$y=-x-1.$$

Это уравнение прямой с угловым коэффициентом $1$, которая пересекает ось $y$ в точке $(0,-1)$ и ось $x$ в точке $(-1,0)$.

График:

График функции $\mathrm{\mid }x\mathrm{\mid }+\mathrm{\mid }y\mathrm{\mid }=1$ будет ромбом с вершинами в точках $(1,0)$, $(0,1)$, $(-1,0)$, и $(0,-1)$.

б) $\mathrm{\mid }x\mathrm{\mid }-\mathrm{\mid }y\mathrm{\mid }=1$

Это уравнение описывает другую геометрическую фигуру, которая будет выглядеть по-другому, поскольку теперь модуль $x$ будет уменьшать модуль $y$, а не увеличивать его.

1. Рассмотрим случай $x\ge 0$ и $y\ge 0$:

В этом случае $\mathrm{\mid }x\mathrm{\mid }=x$ и $\mathrm{\mid }y\mathrm{\mid }=y$, и уравнение превращается в:

$$x-y=1.$$

Решим его относительно $y$:

$$y=x-1.$$

Это уравнение прямой с угловым коэффициентом $1$, которая пересекает ось $y$ в точке $(0,-1)$ и ось $x$ в точке $(1,0)$.

2. Рассмотрим случай $x\ge 0$ и $y\le 0$:

Здесь $x$ остаётся положительным, а $y$ отрицателен, поэтому $\mathrm{\mid }y\mathrm{\mid }=-y$. Уравнение $\mathrm{\mid }x\mathrm{\mid }-\mathrm{\mid }y\mathrm{\mid }=1$ превращается в:

$$x+y=1.$$

Решим его относительно $y$:

$$y=-x+1.$$

Это уравнение прямой с угловым коэффициентом $-1$, которая пересекает ось $y$ в точке $(0,1)$ и ось $x$ в точке $(1,0)$.

3. Рассмотрим случай $x\le 0$ и $y\ge 0$:

Здесь $x$ отрицателен, а $y$ положителен, поэтому $\mathrm{\mid }x\mathrm{\mid }=-x$ и $\mathrm{\mid }y\mathrm{\mid }=y$. Уравнение $\mathrm{\mid }x\mathrm{\mid }-\mathrm{\mid }y\mathrm{\mid }=1$ превращается в:

$$-x-y=1.$$

Решим его относительно $y$:

$$y=-x-1.$$

Это уравнение прямой с угловым коэффициентом $-1$, которая пересекает ось $y$ в точке $(0,-1)$ и ось $x$ в точке $(-1,0)$.

4. Рассмотрим случай $x\le 0$ и $y\le 0$:

Здесь оба значения $x$ и $y$ отрицательны, поэтому $\mathrm{\mid }x\mathrm{\mid }=-x$ и $\mathrm{\mid }y\mathrm{\mid }=-y$. Уравнение $\mathrm{\mid }x\mathrm{\mid }-\mathrm{\mid }y\mathrm{\mid }=1$ превращается в:

$$-x+y=1.$$

Решим его относительно $y$:

$$y=x+1.$$

Это уравнение прямой с угловым коэффициентом $1$, которая пересекает ось $y$ в точке $(0,1)$ и ось $x$ в точке $(-1,0)$.

График:

График функции $\mathrm{\mid }x\mathrm{\mid }-\mathrm{\mid }y\mathrm{\mid }=1$ будет иметь вид четырёх прямых, пересекающихся в точках, которые образуют углы, и будет симметричен относительно осей.