ГДЗ по Алгебре 8 Класс Номер 627 Дорофеев, Суворова — Подробные Ответы

а) Парусная лодка в некоторый момент времени находится в 20 км от наблюдателя и движется в направлении к нему со скоростью 9 км/ч.
1) Обозначьте расстояние между лодкой и наблюдателем (в километрах) буквой y, а время движения лодки в часах) буквой x и составьте уравнение, связывающее y и x. Определите значение y при x=2, x=-1, x=3. Прокомментируйте в соответствии с условием задачи каждый ответ.
2) Постройте график уравнения.
б) После сильных дождей вода в реке поднялась над обычным уровнем на 1,5 м. Через некоторое время уровень начал снижаться в среднем на 20 см в час.
1) Обозначьте высоту воды над обычным уровнем (в метрах) буквой y, а время снижения уровня воды (в часах) буквой x и составьте уравнение, связывающее y и x. Определите, на какой высоте над обычным уровнем окажется вода через 4 ч после начала снижения; через какое время вода достигнет обычного уровня.
2) Постройте график уравнения.

а) 1) Пусть расстояние между лодкой и наблюдателем $y$ км, а время движения лодки $x$ ч.
Составим уравнение:

$$y=20-9x\mathrm{.}$$

при $x=2$ ч:

$$y=20-9\cdot 2=20-18=2(\text{км})\text{— то есть, через 2 ч лодка будет в 2 км от наблюдателя.}$$

при $x=-1$ ч:

$$y=20-9\cdot (-1)=20+9=29(\text{км})\text{— то есть, за час до указанного}$$

$$\text{ момента лодка будет в 29 км от наблюдателя.}$$

при $x=3$ ч:

$$y=20-9\cdot 3=20-27=-7(\text{км})\text{— то есть, через 3 ч лодка}$$

$$\text{ удалится от наблюдателя на 7 км.}$$

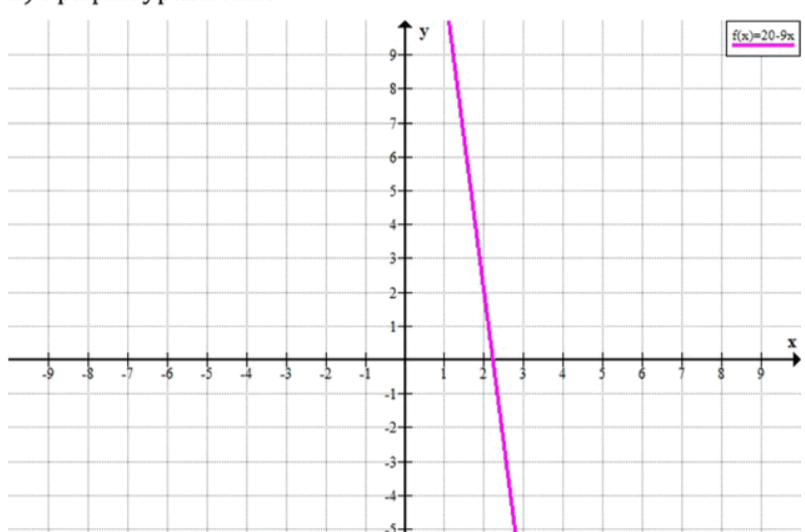
2) График уравнения:

б) 1) Пусть высота воды над обычным уровнем $y$ м, а время снижения уровня воды $x$ ч.
$20\text{ см}=0.2\text{ м}$.
Составим уравнение:

$$y=1.5-0.2x\mathrm{.}$$

при $x=4$ ч:

$$y=1.5-0.2\cdot 4=1.5-0.8=0.7(\text{м})\text{— то есть, через 4 ч вода}$$

$$\text{ окажется над обычным уровнем на высоте 0,7 м или 70 см.}$$

Вода достигнет обычного уровня (при $y=0$):

$$0=1.5-0.2x$$

$$0.2x=1.5$$

$$x=7.5(\text{ч})\mathrm{.}$$

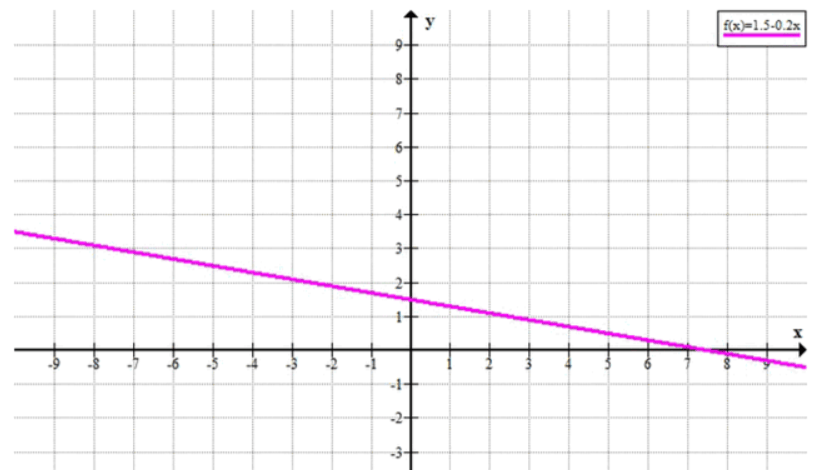
2) График уравнения:

а) Расстояние между лодкой и наблюдателем:

Пусть расстояние между лодкой и наблюдателем $y$ км, а время движения лодки $x$ ч. Из условий задачи составим уравнение для зависимости расстояния от времени:

$$y=20-9x$$

Это уравнение описывает движение лодки, где $y$ — это расстояние от наблюдателя, а $x$ — время, прошедшее с момента начала наблюдения.

Рассмотрим разные значения времени $x$:

При $x=2$ ч: Подставим $x=2$ в уравнение:

$$y=20-9\cdot 2=20-18=2(\text{км})$$

Это означает, что через 2 часа лодка будет находиться в 2 км от наблюдателя.

При $x=-1$ ч: Подставим $x=-1$ в уравнение:

$$y=20-9\cdot (-1)=20+9=29(\text{км})$$

Это означает, что за час до указанного момента (время $x=-1$) лодка находилась на расстоянии 29 км от наблюдателя.

При $x=3$ ч: Подставим $x=3$ в уравнение:

$$y=20-9\cdot 3=20-27=-7(\text{км})$$

Это означает, что через 3 часа лодка окажется на расстоянии 7 км от наблюдателя, но в противоположную сторону (отрицательное значение).

График уравнения:

График уравнения $y=20-9x$ будет прямой, которая пересекает ось $y$ в точке $(0,20)$ и имеет отрицательный наклон, так как угловой коэффициент $k=-9$.

б) Снижение уровня воды:

Пусть высота воды над обычным уровнем $y$ м, а время снижения уровня воды $x$ ч. Также $20\text{ см}=0.2\text{ м}$. Составим уравнение зависимости высоты воды от времени:

$$y=1.5-0.2x$$

Это уравнение описывает изменение высоты воды, где $y$ — это высота воды в метрах, а $x$ — время, прошедшее с момента начала наблюдения.

Рассмотрим разные значения времени $x$:

При $x=4$ ч: Подставим $x=4$ в уравнение:

$$y=1.5-0.2\cdot 4=1.5-0.8=0.7(\text{м})$$

Это означает, что через 4 часа уровень воды будет равен 0.7 м (или 70 см) над обычным уровнем.

Когда вода достигнет обычного уровня (при $y=0$): Подставим $y=0$ в уравнение:

$$0=1.5-0.2x$$

Переносим $1.5$ на правую сторону:

$$0.2x=1.5$$

Делим обе стороны на $0.2$:

$$x=\frac{1.5}{0.2}=7.5(\text{ч})\mathrm{.}$$

Это означает, что вода достигнет обычного уровня через 7.5 часов.

График уравнения:

График уравнения $y=1.5-0.2x$ будет прямой с отрицательным наклоном, которая пересекает ось $y$ в точке $(0,1.5)$, и будет опускаться вниз по мере увеличения времени.