
Учебник по Алгебре для 8-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 8 Класс Номер 626 Дорофеев, Суворова — Подробные Ответы
Определите, пересекаются ли данные прямые; если да, постройте их и найдите координаты точки пересечения, проверив результат подстановкой найденных координат в уравнения:
а) и ;
б) и ;
в) и ;
г) и .
а) и :
б) и :
Прямые пересекаются в точке :
Ответ: .
в) и :
Прямые пересекаются в точке :
Ответ: .
г) и :
а) и :
Для нахождения точки пересечения этих прямых нужно приравнять их уравнения и решить для .
Приравниваем уравнения:
Решение:
Переходим к решению уравнения. В данном случае видим, что из обеих сторон уравнения сокращаются, и остается:
Это неверно, что означает, что уравнение не имеет решения.
Заключение:
Так как полученное выражение невозможно, это свидетельствует о том, что прямые не пересекаются.
Ответ: Прямые не пересекаются.
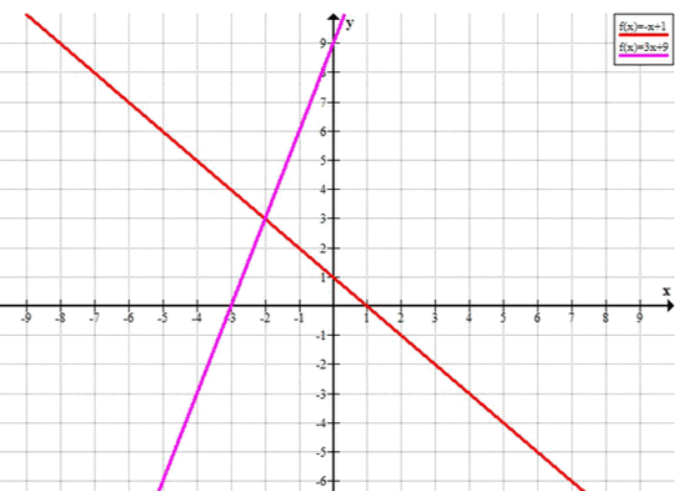
б) и :
Приравниваем уравнения:
Для нахождения точки пересечения приравниваем правые части уравнений:
Решение для :
Переносим все члены с на одну сторону, а все константы — на другую:
Разделим обе стороны на , чтобы выразить :
Решение для :
Теперь подставляем в одно из уравнений (например, ):
Ответ:
Прямые пересекаются в точке .
График пересечения:
Ответ: .
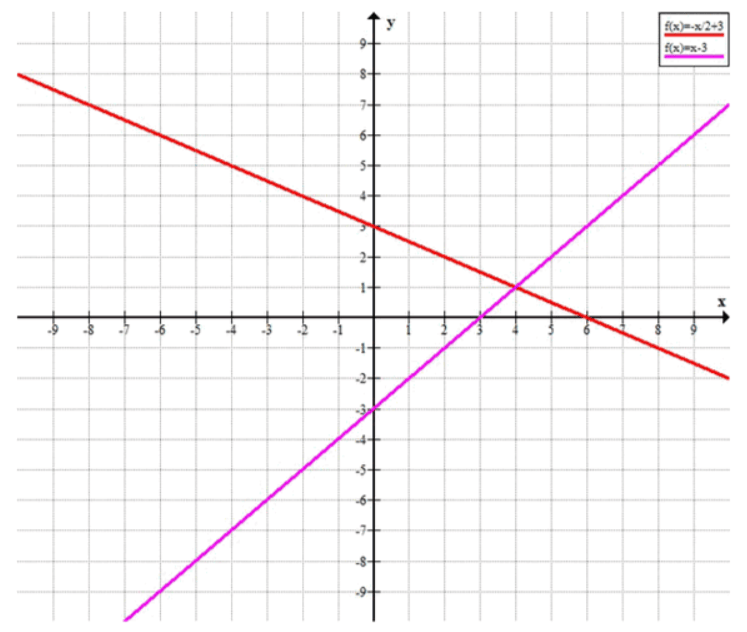
в) и :
Приравниваем уравнения:
Приравниваем правые части уравнений:
Решение для :
Переносим все члены с на одну сторону и константы на другую:
Преобразуем в дробь:
Умножаем обе стороны на , чтобы выразить :
Решение для :
Подставляем в одно из уравнений (например, ):
Ответ:
Прямые пересекаются в точке .
График пересечения:
Ответ: .
г) и :
Приравниваем уравнения:
Приравниваем правые части уравнений:
Решение:
Здесь видно, что сокращается с обеих сторон:
Это неверно, что означает, что прямые не пересекаются.
Заключение:
Так как полученное выражение невозможно, это свидетельствует о том, что прямые не пересекаются.
Ответ: Прямые не пересекаются.




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!