ГДЗ по Алгебре 8 Класс Номер 611 Дорофеев, Суворова — Подробные Ответы

Выпишите уравнения, графиками которых являются прямые, проходящие через начало координат, и постройте эти прямые:
$y=3x^2,y=\frac{x}{4},y=4x-1,y=\frac{2}{x},y=-3x,y=-5$.

График прямой, проходящей через начало координат, имеет вид: $y=kx$.

Выпишем такие графики:

$$y=\frac{x}{4},y=-3x;$$

Шаг 1: Общий вид уравнения прямой

Уравнение прямой, проходящей через начало координат, всегда имеет вид:

$$y=kx$$

где:

• $k$ — это угловой коэффициент, который определяет наклон прямой.
• $x$ и $y$ — переменные, представляющие координаты точек на графике прямой.
• Так как прямая проходит через начало координат $(0;0)$, то свободный член $l=0$, и уравнение не содержит сдвигов по осям.

Шаг 2: Рассмотрим уравнение $y=\frac{x}{4}$

Это уравнение имеет вид:

$$y=\frac{1}{4}x$$

Угловой коэффициент:

• $k=\frac{1}{4}$ — это угловой коэффициент, который указывает, как изменяется $y$ при изменении $x$. Чем больше значение $k$, тем более крутым будет наклон прямой. В данном случае $k$ положительное, что означает, что прямая наклонена вверх слева направо.

Характеристики прямой:

• Когда $x=0$, то $y=0$, то есть прямая проходит через начало координат $(0;0)$.
• Для каждого шага по оси $x$, значение $y$ изменяется на $\frac{1}{4}$ от изменения $x$.
• Например, при $x=4$, $y=1$; при $x=8$, $y=2$; при $x=-4$, $y=-1$.

График:

• Прямая будет плавно подниматься с наклоном $\frac{1}{4}$, то есть за каждый шаг по оси $x$ на 4 единицы, $y$ будет увеличиваться на 1 единицу.
• Прямая будет проходить через точки $(0;0)$, $(4;1)$, $(8;2)$, $(-4;-1)$, и так далее.

Шаг 3: Рассмотрим уравнение $y=-3x$

Это уравнение имеет вид:

$$y=-3x$$

Угловой коэффициент:

• $k=-3$ — это угловой коэффициент, который указывает, как изменяется $y$ при изменении $x$. В данном случае $k$ отрицательное, что означает, что прямая наклонена вниз слева направо.
• Чем больше по абсолютной величине значение $k$, тем более крутым будет наклон прямой. Здесь наклон более крутой по сравнению с предыдущей прямой, так как $k=-3$.

Характеристики прямой:

• Когда $x=0$, то $y=0$, то есть прямая также проходит через начало координат $(0;0)$.
• Для каждого шага по оси $x$, значение $y$ изменяется на $-3$ от изменения $x$.
• Например, при $x=1$, $y=-3$; при $x=-1$, $y=3$; при $x=2$, $y=-6$.

График:

• Прямая будет опускаться с наклоном $-3$, то есть за каждый шаг по оси $x$ на 1 единицу, $y$ будет уменьшаться на 3 единицы.
• Прямая будет проходить через точки $(0;0)$, $(1;-3)$, $(2;-6)$, $(-1;3)$, и так далее.

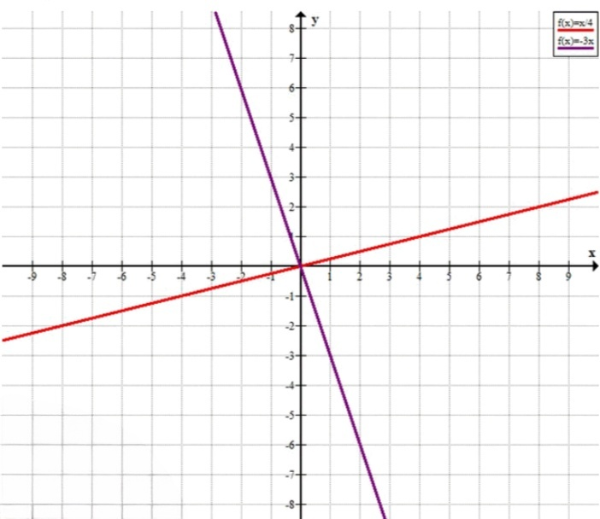
Шаг 4: Общее описание графиков

Для уравнения $y=\frac{x}{4}$:

• Прямая имеет положительный наклон.
• Угловой коэффициент $k=\frac{1}{4}$ указывает на медленный рост $y$ по отношению к $x$.
• Прямая плавно поднимется, проходя через такие точки, как $(0;0)$, $(4;1)$, $(-4;-1)$.

Для уравнения $y=-3x$:

• Прямая имеет отрицательный наклон.
• Угловой коэффициент $k=-3$ указывает на крутой спуск прямой.
• Прямая круто опускается, проходя через такие точки, как $(0;0)$, $(1;-3)$, $(-1;3)$.