ГДЗ по Алгебре 8 Класс Номер 598 Дорофеев, Суворова — Подробные Ответы

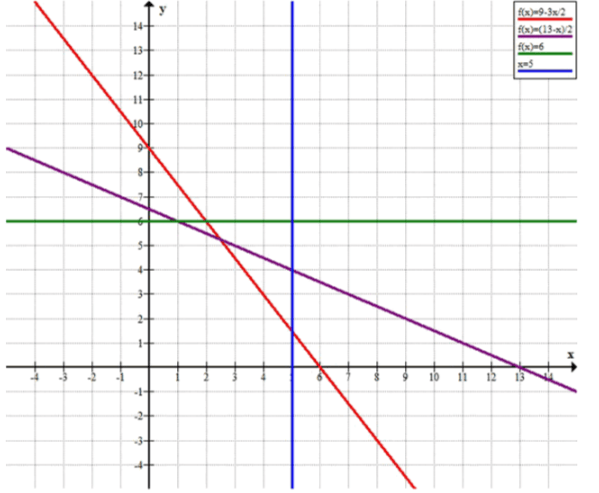
Постройте в одной и той же системе координат следующие прямые: 3x+2y-18=0, x+2y-13=0, 3x-15=0, 2y-12=0.
Определите координаты точек пересечения:
а) прямых 3x+2y-18=0 и 2y-12=0;
б) прямых x+2y-13=0 и 3x-15=0.

$$3x+2y-18=0$$

$$2y=18-3x$$

$$y=9-\frac{3}{2}x$$

$$x+2y-13=0,$$

$$2y=13-x$$

$$y=\frac{13}{2}-\frac{x}{2}$$

$$3x-15=0,$$

$$3x=15$$

$$x=5.$$

$$2y-12=0$$

$$2y=12$$

$$y=6.$$

а) $3x+2y-18=0$ и $2y-12=0$;

Координата точки пересечения $(2;6)$.

б) $x+2y-13=0$ и $3x-15=0$;

Координата точки пересечения $(5;4)$.

а) $3x+2y-18=0$ и $2y-12=0$

1. Решение уравнения $3x+2y-18=0$

Для начала, перепишем уравнение в виде выражения для $y$:

$$3x+2y-18=0$$

Переносим все члены, не содержащие $y$, в правую часть уравнения:

$$2y=18-3x$$

Делим обе стороны на 2:

$$y=9-\frac{3}{2}x$$

Теперь у нас есть уравнение прямой, выраженное через $y$: $y=9-\frac{3}{2}x$.

2. Построение таблицы значений для уравнения $y=9-\frac{3}{2}x$

Для построения таблицы значений подставим несколько значений $x$ и найдем соответствующие значения $y$.

• Для $x=0$:

$$y=9-\frac{3}{2}\cdot 0=9$$

• Для $x=2$:

$$y=9-\frac{3}{2}\cdot 2=9-3=6$$

Таблица значений:

3. Решение уравнения $2y-12=0$

Теперь перейдем ко второму уравнению:

$$2y-12=0$$

Переносим все члены, не содержащие $y$, в правую часть уравнения:

$$2y=12$$

Делим обе стороны на 2:

$$y=6$$

4. Нахождение точки пересечения

Теперь у нас есть два уравнения:

$y=9-\frac{3}{2}x$

$y=6$

Подставим $y=6$ во первое уравнение:

$$6=9-\frac{3}{2}x$$

Переносим $9$ в левую часть уравнения:

$$6-9=-\frac{3}{2}x$$$$-3=-\frac{3}{2}x$$

Умножим обе стороны на $-\frac{2}{3}$:

$$x=2$$

Теперь, зная $x=2$, подставим его во второе уравнение $y=6$. Таким образом, точка пересечения этих двух прямых — $(2;6)$.

Ответ для пункта а:

Точка пересечения: $(2;6)$

б) $x+2y-13=0$ и $3x-15=0$

1. Решение уравнения $x+2y-13=0$

Перепишем уравнение в виде выражения для $y$:

$$x+2y-13=0$$

Переносим все члены, не содержащие $y$, в правую часть уравнения:

$$2y=13-x$$

Делим обе стороны на 2:

$$y=\frac{13}{2}-\frac{x}{2}$$

Теперь у нас есть уравнение прямой, выраженное через $y$: $y=\frac{13}{2}-\frac{x}{2}$.

2. Построение таблицы значений для уравнения $y=\frac{13}{2}-\frac{x}{2}$

Для построения таблицы значений подставим несколько значений $x$ и найдем соответствующие значения $y$.

• Для $x=1$:

$$y=\frac{13}{2}-\frac{1}{2}=\frac{12}{2}=6$$

• Для $x=3$:

$$y=\frac{13}{2}-\frac{3}{2}=\frac{10}{2}=5$$

Таблица значений:

3. Решение уравнения $3x-15=0$

Теперь решим второе уравнение:

$$3x-15=0$$

Переносим все члены, не содержащие $x$, в правую часть уравнения:

$$3x=15$$

Делим обе стороны на 3:

$$x=5$$

4. Нахождение точки пересечения

Теперь у нас есть два уравнения:

$y=\frac{13}{2}-\frac{x}{2}$

$x=5$

Подставим $x=5$ в первое уравнение:

$$y=\frac{13}{2}-\frac{5}{2}=\frac{8}{2}=4$$

Таким образом, точка пересечения этих двух прямых — $(5;4)$.

Ответ для пункта б:

Точка пересечения: $(5;4)$