ГДЗ по Алгебре 8 Класс Номер 394 Дорофеев, Суворова — Подробные Ответы

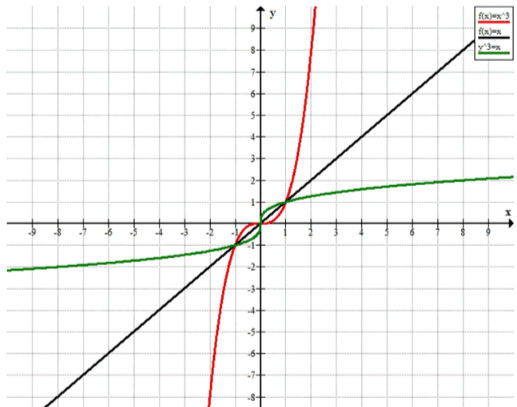
В одной системе координат постройте графики зависимостей $y = x^3$ и $y = \sqrt[3]{x}$. Как расположены относительно прямой $y = x$ графики этих зависимостей?

$y=x^3$, $y=\sqrt[3]{x}$;

Графики $y=x^3$ и $y=\sqrt[3]{x}$ расположены симметрично относительно прямой $y=x$.

Функции $y=x^3$ и $y=\sqrt[3]{x}$:

У нас есть две функции:

$y=x^3$ — кубическая функция.

$y=\sqrt[3]{x}$ — кубический корень из $x$, то есть обратная функция для $y=x^3$.

Мы хотим доказать, что графики этих функций расположены симметрично относительно прямой $y=x$.

Симметрия графиков относительно прямой $y=x$:

Симметрия относительно прямой $y=x$ означает, что для каждой точки на графике одной функции существует точка на графике другой функции, которая симметрична ей относительно этой прямой.

Чтобы это доказать, нужно показать, что если точка $(a,b)$ лежит на графике функции $y=x^3$, то точка $(b,a)$ лежит на графике функции $y=\sqrt[3]{x}$, и наоборот.

Проверим симметрию:

Пусть точка $(a,b)$ лежит на графике функции $y=x^3$. Это означает, что $b=a^3$.

Рассмотрим точку $(b,a)$. Чтобы эта точка лежала на графике функции $y=\sqrt[3]{x}$, должно выполняться следующее: $a=\sqrt[3]{b}$.

Мы знаем, что $b=a^3$, следовательно $a=\sqrt[3]{b}$ верно, так как $a=\sqrt[3]{a^3}$.

Таким образом, если точка $(a,b)$ лежит на графике функции $y=x^3$, то точка $(b,a)$ лежит на графике функции $y=\sqrt[3]{x}$, и наоборот.

Вывод:

Графики функций $y=x^3$ и $y=\sqrt[3]{x}$ действительно расположены симметрично относительно прямой $y=x$. Это подтверждается тем, что для каждой точки на одном графике существует точка на другом графике, которая симметрична ей относительно прямой $y=x$.

Таким образом, мы доказали, что графики $y=x^3$ и $y=\sqrt[3]{x}$ симметричны относительно прямой $y=x$.