ГДЗ по Алгебре 8 Класс Номер 283 Дорофеев, Суворова — Подробные Ответы

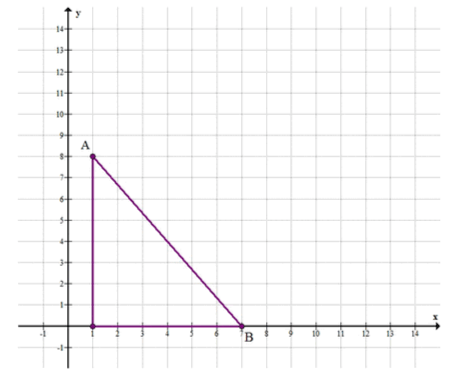
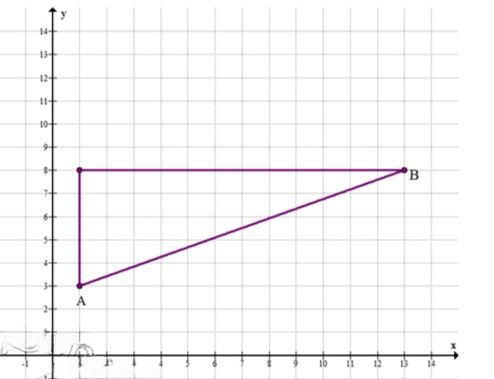
На координатной плоскости отмечены точки A и B. Найдите расстояние между этими точками, если известны их координаты (сделайте рисунок):
1) A (1; 8), B (7; 0);
2) A (1; 3), B (13; 8);
3) A (80; 54), B (83; 50).

$A(1; 8), B(7; 0)$

$AB = \sqrt{8^2 + 6^2} = \sqrt{64 + 36} = \sqrt{100} = 10$

$A(1; 3), B(13; 8)$

$AB = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13$

$A(80; 54), B(83; 50)$

$AB = \sqrt{4^2 + 3^2} = \sqrt{16 + 9} = \sqrt{25} = 5$

$A(1; 8), B(7; 0)$
Чтобы найти расстояние между точками $A(1; 8)$ и $B(7; 0)$, используем формулу для расстояния между двумя точками на плоскости:

$$AB = \sqrt{(x_2 — x_1)^2 + (y_2 — y_1)^2}$$

Подставим значения координат точек $A(1; 8)$ и $B(7; 0)$ в формулу:

$$AB = \sqrt{(7 — 1)^2 + (0 — 8)^2} = \sqrt{6^2 + (-8)^2}$$

Вычислим квадраты:

$$AB = \sqrt{36 + 64} = \sqrt{100}$$

Итак, расстояние между точками $A$ и $B$ равно:

$$AB = 10$$

$A(1; 3), B(13; 8)$
Для нахождения расстояния между точками $A(1; 3)$ и $B(13; 8)$ снова используем формулу для расстояния между двумя точками на плоскости:

$$AB = \sqrt{(x_2 — x_1)^2 + (y_2 — y_1)^2}$$

Подставим значения координат точек $A(1; 3)$ и $B(13; 8)$:

$$AB = \sqrt{(13 — 1)^2 + (8 — 3)^2} = \sqrt{12^2 + 5^2}$$

Вычислим квадраты:

$$AB = \sqrt{144 + 25} = \sqrt{169}$$

Итак, расстояние между точками $A$ и $B$ равно:

$$AB = 13$$

$A(80; 54), B(83; 50)$
Для нахождения расстояния между точками $A(80; 54)$ и $B(83; 50)$ используем ту же формулу для расстояния между двумя точками на плоскости:

$$AB = \sqrt{(x_2 — x_1)^2 + (y_2 — y_1)^2}$$

Подставим значения координат точек $A(80; 54)$ и $B(83; 50)$:

$$AB = \sqrt{(83 — 80)^2 + (50 — 54)^2} = \sqrt{3^2 + (-4)^2}$$

Вычислим квадраты:

$$AB = \sqrt{9 + 16} = \sqrt{25}$$

Итак, расстояние между точками $A$ и $B$ равно:

$$AB=5$$

$$AB = 5$$