ГДЗ по Алгебра 7 Класс Проверьте себя Глава 2 Дорофеев, Суворова — Подробные Ответы

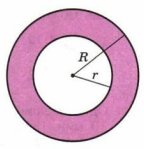
1. Площадь кольца \(S\) можно вычислить по формуле \(S=\pi(R^2-r^2)\). Найдите площадь кольца, если \(R=6\) см, \(r=4\) см (\(\pi\approx3{,}14\)).

2. Клиент банка внёс \(x\) рублей на вклад, по которому вложенная сумма увеличивается на 5% за год, и \(y\) рублей на вклад, по которому начисляется 8% годовых. Через год его доход по двум вкладам составил \(C\) рублей. Какая формула выражает зависимость \(C\) от \(x\) и \(y\)?
1) \(C=0{,}13(x+y)\)
2) \(C=0{,}05x+0{,}08y\)
3) \(C=0{,}5x+0{,}8y\)
4) \(C=5x+8y\)

3. Из геометрической формулы \(S=\frac{ah}{2}\) выразите переменную \(h\).

4. Междугородний автобус проезжает 1 км по шоссе за 50 с. Найдите скорость автобуса в километрах в час.

5. Формула \(P=pt\) связывает три величины: объём выполненной работы \(P\), производительность \(p\) и время выполнения работы \(t\). Какие из следующих утверждений являются верными?
А. Объём выполненной работы при постоянной производительности пропорционален времени работы.
Б. Время работы при постоянном её объёме пропорционально производительности.
В. Объём выполненной работы при постоянном времени работы пропорционален производительности.

6. Автомобиль, двигаясь с постоянной скоростью, за определённое время проехал \(\frac{1}{3}\) всего расстояния до пункта назначения. Какую часть этого расстояния можно было бы проехать за это же время со скоростью, в 1,2 раза большей?

7. Для школы купили 6 одинаковых компьютеров. Сколько компьютеров, стоимость которых в 1,5 раза меньше, можно было бы купить на эту же сумму?
1) 4
2) 8
3) 9
4) для ответа не хватает данных

8. Из каких отношений нельзя составить пропорцию?
1) \(2:7\) и \(11:33\)
2) \(\frac{1}{3}:\frac{1}{4}\) и \(2:\frac{1}{2}\)
3) \(0{,}1:7\) и \(0{,}5:35\)
4) \(0{,}02:0{,}1\) и \(2:10\)

9. Дана пропорция \(5:a=6:b\). Какое из следующих равенств пропорцией не является?
1) \(a:b=5:6\)
2) \(b:a=6:5\)
3) \(a:b=6:5\)
4) \(a:5=b:6\)

10. Как можно найти неизвестный член пропорции \(\frac{x}{1{,}2}=\frac{5}{8}\)?
1) \(x=\frac{8\cdot1{,}2}{5}\)
2) \(x=\frac{1{,}2\cdot5}{8}\)
3) \(x=\frac{8\cdot5}{1{,}2}\)
4) \(x=\frac{8}{1{,}2\cdot5}\)

11. Одна машинистка печатает страницу за 6 мин, а другая — за 10 мин. Первая за некоторое время напечатала 40 страниц. Сколько страниц за это же время напечатает вторая?
Установите, какая пропорция соответствует условию задачи (\(x\) — число страниц, которое напечатает вторая машинистка).
1) \(\frac{6}{10}=\frac{x}{40}\)
2) \(\frac{6}{10}=\frac{40}{x}\)
3) \(\frac{6}{40}=\frac{x}{10}\)
4) \(\frac{6}{40}=\frac{10}{x}\)

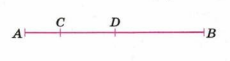
12. Отрезок \(AB\), длина которого равна 21 см, точками \(C\) и \(D\) разделён на три части в отношении \(2:3:5\). Чему равна длина отрезка \(CB\)?

1. \(S=\pi(R^2-r^2)=3{,}14(6^2-4^2)=3{,}14\cdot20=62{,}8\ \text{см}^2\).
Ответ: \(62{,}8\ \text{см}^2\).

2. Доход за год: \(C=0{,}05x+0{,}08y\).
Ответ: 2.

3. Из \(S=\frac{ah}{2}\) получаем \(ah=2S\), значит \(h=\frac{2S}{a}\).

4. \(1:50=0{,}02\ \text{км/с}\), тогда \(0{,}02\cdot60\cdot60=72\ \text{км/ч}\).
Ответ: \(72\ \text{км/ч}\).

5. При \(P=pt\): при постоянном \(p\) \(P\) пропорционален \(t\) (А — верно); при постоянном \(P\) \(t=\frac{P}{p}\), то есть обратно пропорционален \(p\) (Б — неверно); при постоянном \(t\) \(P\) пропорционален \(p\) (В — верно).
Ответ: верны утверждения А и В.

6. При одинаковом времени путь пропорционален скорости: \(1{,}2\cdot\frac{1}{3}=0{,}4\).
Ответ: \(0{,}4\) расстояния.

7. Если цена в \(1{,}5\) раза меньше, то на ту же сумму купят в \(1{,}5\) раза больше: \(6\cdot1{,}5=9\).
Ответ: 9.

8. Проверка равенства отношений:
1) \(\frac{2}{7}\neq\frac{11}{33}\), пропорцию составить нельзя;
2) отношения не равны, пропорцию составить нельзя;
3) и 4) отношения равны, составить можно.
Ответ: пропорцию нельзя составить из соотношений 1 и 2.

9. Из \(5:a=6:b\) следует \(5b=6a\), тогда \(a:b=5:6\) верно, \(b:a=6:5\) верно, а \(a:b=6:5\) неверно.
Ответ: 3.

10. \(\frac{x}{1{,}2}=\frac{5}{8}\Rightarrow 8x=1{,}2\cdot5\Rightarrow x=\frac{5\cdot1{,}2}{8}\).
Ответ: 2.

11. За одинаковое время число страниц обратно пропорционально времени на страницу: \(\frac{6}{10}=\frac{x}{40}\Rightarrow 10x=6\cdot40\Rightarrow x=\frac{6\cdot40}{10}=24\).
Ответ: условию задачи соответствует пропорция 1.

12. Одна часть: \(21:(2+3+5)=21:10=2{,}1\ \text{см}\); \(CB\) — это \((3+5)\) частей: \(2{,}1\cdot8=16{,}8\ \text{см}\).
Ответ: \(16{,}8\ \text{см}\).

1. Площадь кольца — это разность площадей двух кругов: большого радиуса \(R\) и малого радиуса \(r\). Поэтому используем формулу \(S=\pi(R^{2}-r^{2})\), где \(R^{2}\) и \(r^{2}\) — квадраты радиусов, а \(\pi\) дано как \(3{,}14\). Подставляем \(R=6\), \(r=4\): \(S=3{,}14(6^{2}-4^{2})=3{,}14(36-16)=3{,}14\cdot20=62{,}8\ \text{см}^{2}\). Ответ: \(62{,}8\ \text{см}^{2}\).

2. «Доход» по вкладу — это начисленные проценты за год, то есть доля от вложенной суммы. Если на вклад \(x\) начисляют 5% годовых, то доход с него равен \(0{,}05x\). Если на вклад \(y\) начисляют 8% годовых, то доход с него равен \(0{,}08y\). Общий доход за год по двум вкладам складывается: \(C=0{,}05x+0{,}08y\). Ответ: 2.

3. В формуле \(S=\frac{ah}{2}\) переменная \(h\) умножается на \(a\) и затем делится на 2. Чтобы выразить \(h\), сначала избавляемся от деления на 2: умножаем обе части на 2 и получаем \(2S=ah\). Затем делим обе части на \(a\), чтобы \(h\) осталось отдельно: \(h=\frac{2S}{a}\). Это и есть выражение высоты через площадь и основание.

4. Скорость — это расстояние, делённое на время. Здесь за \(50\) секунд автобус проезжает \(1\) км, значит скорость в км/с равна \(v=\frac{1}{50}\ \text{км/с}=0{,}02\ \text{км/с}\). Чтобы перевести км/с в км/ч, учитываем, что в 1 часе \(60\cdot60=3600\) секунд: \(v=0{,}02\cdot60\cdot60=72\ \text{км/ч}\). Ответ: \(72\ \text{км/ч}\).

5. Формула \(P=pt\) означает: объём работы \(P\) равен производительности \(p\), умноженной на время \(t\). Если \(p\) постоянна, то \(P\) меняется прямо пропорционально \(t\): чем больше времени, тем больше выполнено работы, это утверждение А верно. Если \(P\) фиксирован, то \(t=\frac{P}{p}\), то есть время обратно пропорционально производительности, поэтому утверждение Б (про прямую пропорциональность) неверно. Если \(t\) постоянно, то \(P=pt\) показывает, что \(P\) прямо пропорционален \(p\), значит утверждение В верно. Ответ: верны утверждения А и В.

6. За одно и то же время пройденное расстояние прямо пропорционально скорости: если скорость увеличить в \(1{,}2\) раза, то за тот же промежуток времени проедут в \(1{,}2\) раза больше пути. По условию при старой скорости за это время проехали \(\frac{1}{3}\) всего расстояния, значит при новой скорости проедут \(1{,}2\cdot\frac{1}{3}\). Вычисляем: \(1{,}2\cdot\frac{1}{3}=0{,}4\). Ответ: \(0{,}4\) расстояния.

7. Пусть цена одного компьютера равна \(p\). Тогда на 6 одинаковых компьютеров потратили \(6p\). Если новые компьютеры «в 1,5 раза меньше по стоимости», это означает, что их цена равна \(\frac{p}{1{,}5}\). На ту же сумму \(6p\) можно купить \(n\) таких компьютеров: \(n\cdot\frac{p}{1{,}5}=6p\). Делим на \(p\): \(\frac{n}{1{,}5}=6\), значит \(n=6\cdot1{,}5=9\). Ответ: 9.

8. Пропорцию можно составить только из равных отношений, то есть когда \(\frac{a}{b}=\frac{c}{d}\). Для пункта 1 проверяем: \(\frac{2}{7}\) и \(\frac{11}{33}\) не равны, потому что \(\frac{11}{33}=\frac{1}{3}\), а \(\frac{2}{7}\neq\frac{1}{3}\), значит составить нельзя. Для пункта 2 аналогично отношения не равны, значит тоже нельзя. Для пункта 3: \(\frac{0{,}1}{7}=\frac{1}{70}\) и \(\frac{0{,}5}{35}=\frac{1}{70}\), равны — составить можно; для пункта 4: \(\frac{0{,}02}{0{,}1}=0{,}2\) и \(\frac{2}{10}=0{,}2\), тоже можно. Ответ: пропорцию нельзя составить из соотношений 1 и 2.

9. Дано \(5:a=6:b\), это означает равенство дробей \(\frac{5}{a}=\frac{6}{b}\), а при перемножении крест-накрест получаем \(5b=6a\). Из \(5b=6a\) следует \(\frac{a}{b}=\frac{5}{6}\), то есть верно \(a:b=5:6\) и верно \(b:a=6:5\). Равенство \(a:b=6:5\) означало бы \(\frac{a}{b}=\frac{6}{5}\), что противоречит \(\frac{a}{b}=\frac{5}{6}\), поэтому оно пропорцией не является. Ответ: 3.

10. В пропорции \(\frac{x}{1{,}2}=\frac{5}{8}\) неизвестный член \(x\) находят по правилу: произведение крайних равно произведению средних. Крайние здесь \(x\) и \(8\), средние \(1{,}2\) и \(5\), значит \(8x=1{,}2\cdot5\). Отсюда \(x=\frac{1{,}2\cdot5}{8}\), то есть верный способ соответствует варианту, где записано \(8x=1{,}2\cdot5\) и затем \(x=\frac{5\cdot1{,}2}{8}\). Ответ: 2.

11. Первая печатает 1 страницу за 6 минут, вторая — за 10 минут, значит за одинаковое время число страниц обратно пропорционально времени на одну страницу. Если за некоторое время первая сделала 40 страниц, то это время равно \(40\cdot6\) минут. За то же время вторая напечатает \(x\) страниц, значит \(x\cdot10=40\cdot6\), что соответствует записи \(\frac{6}{10}=\frac{x}{40}\). Именно эта пропорция и является вариантом 1. Ответ: условию задачи соответствует пропорция 1.

12. Отрезок \(AB=21\) см разделён в отношении \(2:3:5\), то есть всего частей \(2+3+5=10\). Длина одной «части» равна \(\frac{21}{10}=2{,}1\) см. Отрезок \(CB\) включает две последние части (от \(C\) до \(D\) — 3 части, от \(D\) до \(B\) — 5 частей), вместе \(3+5=8\) частей, значит \(CB=2{,}1\cdot8=16{,}8\) см. Ответ: \(16{,}8\ \text{см}\).