
Учебник «Алгебра. 7 класс» авторов Дорофеев Г.В. и Суворова С.Б. — это современное пособие, которое помогает школьникам сделать первые серьезные шаги в изучении алгебры. Книга рассчитана на широкий круг учеников и отличается продуманной структурой, доступным языком и большим количеством разнообразных задач.
ГДЗ по Алгебра 7 Класс Проверьте себя Глава 5 Дорофеев, Суворова — Подробные Ответы
1. Поставьте в соответствие каждому промежутку его алгебраическое описание.
A) \(x>-2\)
Б) \(x\le-2\)
B) \(x>-6\)
Г) \(x\le-6\)
2. Укажите число, не принадлежащее промежутку \(-0,25 < x < 0,55\).
1) \(\frac{1}{2}\) 2) \(\frac{1}{4}\) 3) \(\frac{-1}{3}\) 4) \(-\frac{1}{5}\)
3. На координатной прямой отмечены точки \(A(-1,5)\) и \(B(6)\). Найдите координату точки \(M\), если известно, что \(AM : MB = 1 : 2\).
4. Установите соответствие между неравенствами, задающими один и тот же числовой промежуток и расположенными в верхней и в нижней строке.
A) \(4<x<16\)
1) \(|x|<10\) 2) \(|x+5|<3\)
Б) \(-8<x\le-2\)
3) \(|x-10|<6\)
5. Каким равенством можно задать вертикальную прямую, проходящую через точку \(M(-2; 6)\)?
1) \(x=-2\) 2) \(x=6\) 3) \(y=-2\) 4) \(y=6\)
6. Каким равенством можно задать горизонтальную прямую, проходящую через точку \(M(a; b)\)?
1) \(x=a\) 2) \(x=b\) 3) \(y=a\) 4) \(y=b\)
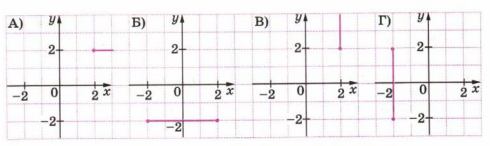
7. Поставьте в соответствие каждому множеству точек его алгебраическое описание.
1) \(x=2\) и \(y>2\) 3) \(y=-2\) и \(|x|<2\)
2) \(y=2\) и \(x>2\) 4) \(x=-2\) и \(|y|<2\)
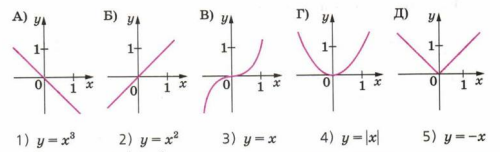
8. Для каждого графика укажите его алгебраическое описание.
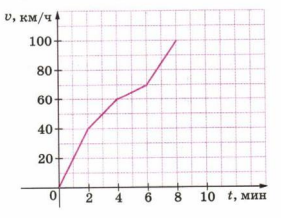
9. На рисунке изображён график изменения скорости автомобиля. Определите, на каком промежутке времени скорость автомобиля росла быстрее.
1) на промежутке от 0 мин до 2 мин
2) на промежутке от 2 мин до 4 мин
3) на промежутке от 4 мин до 6 мин
4) на промежутке от 6 мин до 8 мин
1. А) \(x \le -6\) (4);
Б) \(x \ge -2\) (1);
В) \(x \ge -6\) (3);
Г) \(x \le -2\) (2).
Ответ: А – 4; Б – 1; В – 3; Г – 2.
2. Промежуток: \(-0,25 < x < 0,55\)
1) \(\frac{1}{2} = 0,5\) – принадлежит;
2) \(\frac{1}{4} = 0,25\) – принадлежит;
3) \(-\frac{1}{3} \approx -0,333\) – не принадлежит;
4) \(-\frac{1}{5} = -0,2\) – принадлежит.
Ответ: 3.
3. Даны точки \(A(-1,5)\), \(B(6)\), отношение \(AM : MB = 1 : 2\).
Длина отрезка \(AB = |6 — (-1,5)| = 7,5\).
Длина одной части: \(7,5 : (1+2) = 7,5 : 3 = 2,5\).
Координата \(M = -1,5 + 2,5 = 1\).
Ответ: \(M(1)\).
4. 1) \(|x| < 10\) означает, что \(x\) находится между \(-10\) и \(10\), то есть \(-10 < x < 10\). Это соответствует промежутку Б.
2) \(|x + 5| < 3\) означает, что расстояние между \(x\) и \(-5\) меньше 3, значит \(-3 < x + 5 < 3\). Вычтем 5: \(-8 < x < -2\). Это соответствует промежутку В.
3) \(|x — 10| < 6\) означает, что расстояние между \(x\) и \(10\) меньше 6, значит \(-6 < x — 10 < 6\). Прибавим 10: \(4 < x < 16\). Это соответствует промежутку А.
Ответ: А – 3; Б – 1; В – 2.
5. Вертикальная прямая, проходящая через точку \(M(-2; 6)\), задаётся уравнением \(x = -2\). Это потому, что для вертикальной прямой координата \(x\) постоянна и равна абсциссе точки, через которую она проходит. Ответ: 1.
6. Горизонтальная прямая, проходящая через точку \(M(a; b)\), задаётся уравнением \(y = b\). Для горизонтальной прямой координата \(y\) постоянна и равна ординате точки, через которую она проходит. Ответ: 4.
7. Соответствие множествам точек и уравнениям:
А) \(y = 2\), \(x \ge 2\) – это множество точек, где \(y\) постоянно равно 2, а \(x\) больше или равно 2 (2).
Б) \(y = -2\), \(|x| \le 2\) – горизонтальная линия \(y = -2\), где \(x\) ограничен по модулю (3).
В) \(x = 2\), \(y \ge 2\) – вертикальная линия \(x = 2\), \(y\) больше или равно 2 (1).
Г) \(x = -2\), \(|y| \le 2\) – вертикальная линия \(x = -2\), с ограничением по \(y\) (4).
Ответ: А – 2; Б – 3; В – 1; Г – 4.
8. Соответствие графикам и уравнениям:
А) \(y = -x\) (5) – прямая с отрицательным наклоном.
Б) \(y = x\) (3) – прямая с положительным наклоном.
В) \(y = x^3\) (1) – кубическая функция.
Г) \(y = x^2\) (2) – парабола вверх.
Д) \(y = |x|\) (4) – график модуля.
Ответ: А – 5; Б – 3; В – 1; Г – 2; Д – 4.
9. Рассмотрим скорость на каждом промежутке времени:
1) от 0 до 2 мин – скорость изменилась с 0 до 40 км/ч, прирост 40 км/ч;
2) от 2 до 4 мин – изменение скорости 20 км/ч;
3) от 4 до 6 мин – изменение скорости 10 км/ч;
4) от 6 до 8 мин – изменение скорости 30 км/ч.
Самый быстрый рост скорости на промежутке от 0 до 2 минут. Ответ: 1.
1. Рассмотрим каждое неравенство и соответствующий ему промежуток. В пункте А дано \(x \le -6\), что соответствует промежутку, включающему все числа, меньшие или равные \(-6\). На рисунке этот промежуток обозначен как (4), так как стрелка направлена влево от точки \(-6\) и включает эту точку. В пункте Б указано \(x \ge -2\), что охватывает все числа, начиная с \(-2\) и больше. Это соответствует обозначению (1), где стрелка направлена вправо от точки \(-2\) и точка включена.
В пункте В записано \(x \ge -6\), что значит все числа от \(-6\) и больше. На рисунке это соответствует промежутку (3), где стрелка направлена вправо от \(-6\), включая эту точку. В пункте Г указано \(x \le -2\), что включает все числа меньше или равные \(-2\), что совпадает с промежутком (2) на рисунке, где стрелка направлена влево от \(-2\), включая точку. Таким образом, правильное соответствие: А – 4, Б – 1, В – 3, Г – 2.
2. Дан промежуток \(-0,25 < x < 0,55\), нужно определить, какое из чисел не принадлежит этому промежутку. Рассмотрим каждое число по отдельности. Число \(\frac{1}{2} = 0,5\) находится между \(-0,25\) и \(0,55\), значит оно принадлежит промежутку. Число \(\frac{1}{4} = 0,25\) также лежит в пределах промежутка, так как больше \(-0,25\) и меньше \(0,55\).
Число \(-\frac{1}{3} \approx -0,333\) меньше нижней границы \(-0,25\), следовательно, оно не входит в данный промежуток. Число \(-\frac{1}{5} = -0,2\) больше \(-0,25\) и меньше \(0,55\), значит принадлежит промежутку. Отсюда следует, что именно число \(-\frac{1}{3}\) не принадлежит промежутку. Ответ: 3.
3. Даны точки \(A(-1,5)\) и \(B(6)\) на числовой прямой, а также отношение отрезков \(AM : MB = 1 : 2\). Сначала вычислим длину отрезка \(AB\). Для этого найдём модуль разности координат: \(AB = |6 — (-1,5)| = |7,5| = 7,5\). Это длина всего отрезка между точками \(A\) и \(B\).
Далее, поскольку точка \(M\) делит отрезок \(AB\) в отношении \(1 : 2\), длина части \(AM\) равна одной трети от длины всего отрезка: \(7,5 : (1+2) = 7,5 : 3 = 2,5\). Чтобы найти координату точки \(M\), прибавим длину части \(AM\) к координате точки \(A\): \(-1,5 + 2,5 = 1\). Следовательно, координата точки \(M\) равна 1.
4. Рассмотрим неравенства и их преобразования. Первое: \(|x| < 10\) означает, что \(x\) находится между \(-10\) и \(10\), то есть \(-10 < x < 10\). Это совпадает с промежутком, указанным в пункте Б.
Во втором случае \(|x + 5| < 3\) означает, что расстояние от \(x\) до \(-5\) меньше 3. Раскроем неравенство: \(-3 < x + 5 < 3\). Вычтем 5 из всех частей: \(-8 < x < -2\). Это соответствует промежутку, указанному в пункте В.
В третьем случае \(|x — 10| < 6\) означает, что расстояние от \(x\) до 10 меньше 6. Раскроем неравенство: \(-6 < x — 10 < 6\). Прибавим 10 ко всем частям: \(4 < x < 16\). Это совпадает с промежутком из пункта А. Итоговое соответствие: А – 3, Б – 1, В – 2.
5. Вертикальная прямая — это геометрическое место точек, у которых координата \(x\) постоянна, а координата \(y\) может принимать любые значения. Если прямая проходит через точку \(M(-2; 6)\), то её уравнение фиксирует именно значение \(x\), равное абсциссе точки \(M\). Следовательно, уравнение вертикальной прямой будет иметь вид \(x = -2\). Это означает, что для всех точек на этой прямой абсцисса равна \(-2\), независимо от значения ординаты \(y\). Ответ: 1.
6. Горизонтальная прямая — это множество точек, у которых координата \(y\) постоянна, а координата \(x\) может изменяться. Если эта прямая проходит через точку \(M(a; b)\), то её уравнение фиксирует значение ординаты \(y\), равное \(b\). Таким образом, уравнение горизонтальной прямой имеет вид \(y = b\). Это значит, что все точки на прямой имеют одинаковое значение \(y\), равное \(b\), а значение \(x\) может быть любым. Ответ: 4.
7. Рассмотрим каждое из множеств и их алгебраические описания. В первом случае \(y = 2\), \(x \ge 2\) — это множество точек, где ордината равна 2, а абсцисса не меньше 2. Такое множество представляет собой горизонтальный луч, начинающийся в точке с координатой \(x=2\) и направленный вправо. Это соответствует варианту (2). Во втором случае \(y = -2\), \(|x| \le 2\) — горизонтальная линия с \(y = -2\), ограниченная по \(x\) в пределах от \(-2\) до 2. Это соответствует варианту (3). В третьем случае \(x = 2\), \(y \ge 2\) — вертикальная линия с \(x=2\), ограниченная снизу значением \(y=2\) и направленная вверх. Это вариант (1). В четвёртом случае \(x = -2\), \(|y| \le 2\) — вертикальная линия с \(x = -2\), ограниченная по \(y\) между \(-2\) и 2. Это соответствует варианту (4). Ответ: А – 2; Б – 3; В – 1; Г – 4.
8. Анализируем графики и соответствующие им уравнения. График А — это прямая с отрицательным наклоном, значит уравнение вида \(y = -x\), что соответствует варианту (5). График Б — прямая с положительным наклоном, уравнение \(y = x\), вариант (3). График В — кубическая функция \(y = x^3\), вариант (1), которая имеет характерный изгиб. График Г — парабола \(y = x^2\), вариант (2), которая открывается вверх. График Д — функция модуля \(y = |x|\), вариант (4), что видно по «угловатому» виду графика. Ответ: А – 5; Б – 3; В – 1; Г – 2; Д – 4.
9. Для определения промежутка с наибольшим ростом скорости автомобиля нужно вычислить изменение скорости за каждый интервал времени. На промежутке от 0 до 2 минут скорость увеличилась с 0 до 40 км/ч, то есть прирост составил 40 км/ч. На промежутке от 2 до 4 минут скорость выросла с 40 до 60 км/ч, прирост 20 км/ч. На промежутке от 4 до 6 минут скорость увеличилась с 60 до 70 км/ч, прирост 10 км/ч. На промежутке от 6 до 8 минут скорость возросла с 70 до 100 км/ч, прирост 30 км/ч. Таким образом, максимальный прирост скорости произошёл на первом промежутке времени от 0 до 2 минут. Ответ: 1.


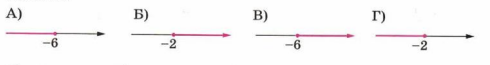


Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!