ГДЗ по Алгебра 7 Класс Проверьте себя Глава 1 Дорофеев, Суворова — Подробные Ответы

1. Какое из данных чисел наименьшее?
1) 0,44 2) 0,8 3) \(\frac{2}{5}\) 4) \(\frac{4}{9}\)

2. Даны дроби \(\frac{1}{a}\) и \(\frac{1}{b}\). Выберите из данных значений \(a\) и \(b\) такие, при которых \(\frac{1}{a}>\frac{1}{b}\).
1) \(a=16,\ b=15\)
2) \(a=-16,\ b=-15\)
3) \(a=-15,\ b=-16\)
4) \(a=-15,\ b=16\)

3. Найдите значение выражения \(\frac{0,3\cdot0,25}{0,45}\).

4. Даны выражения:
1) \(2,37:(1,15\cdot0,18)\).
2) \((2,37:1,15)\cdot0,18\).
3) \(2,37:(1,15:0,18)\).
4) \((2,37:1,15):0,18\).
Укажите номера выражений, которые могут быть преобразованы к виду \(\frac{2,37}{1,15\cdot0,18}\).

5. Найдите значение выражения \(\frac{(a+x)(a-x)}{ax}\) при \(a=-2,\ x=-0,2\).

6. На координатной прямой отмечено число \(a\). Какое из следующих неравенств неверно?
1) \(\frac{1}{a}<-1\)
2) \(-\frac{1}{a}>1\)
3) \(\frac{1}{a}<a\)
4) \(-\frac{1}{a}<a\)

7. Как можно записать короче выражение \(7\cdot7\cdot7\cdot\ldots\cdot7\cdot5\cdot5\cdot5\cdot\ldots\cdot5\)? (10 множителей) (20 множителей)
1) \(7^{10}\cdot5^{20}\)
2) \(7^{10}+5^{20}\)
3) \(10^{7}\cdot20^{5}\)
4) \(10^{7}+20^{5}\)

8. Вычислите \(10\cdot(-0,3)^3\).

9. Расположите в порядке возрастания числа: \(-1,7;\ (-1,7)^2;\ (-1,7)^3\).
1) \(-1,7;\ (-1,7)^2;\ (-1,7)^3\)
2) \((-1,7)^3;\ (-1,7)^2;\ -1,7\)
3) \((-1,7)^3;\ -1,7;\ (-1,7)^2\)
4) \(-1,7;\ (-1,7)^3;\ (-1,7)^2\)

10. Найдите значение выражения \(-(((-1)^{10}-(-1)^{11}))^{2}\).
1) \(-4\) 2) \(-2\) 3) \(0\) 4) \(4\)

11. Соотнесите дроби, которые выражают доли некоторой величины, и соответствующие им проценты.
Дроби: А) \(\frac{3}{5}\) Б) \(\frac{3}{10}\) В) \(0,07\) Г) \(0,7\)
Проценты: 1) \(7\%\) 2) \(60\%\) 3) \(70\%\) 4) \(30\%\)

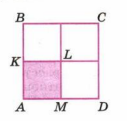
12. На сколько процентов площадь квадрата \(ABCD\) больше площади квадрата \(AKLM\)?

13. На сколько процентов площадь квадрата \(AKLM\) меньше площади квадрата \(ABCD\)?

14. Издательство выпустило 10 наименований книг для взрослых и 40 наименований книг для детей. Сколько процентов всех книг составляют книги для взрослых?
1) \(10\%\) 2) \(15\%\) 3) \(20\%\) 4) \(25\%\)

15. Цена акции за неделю понизилась на \(10\%\) и стала равной 3 р. 60 к. Сколько стоила акция неделю назад?
1) 4 р. 2) 3 р. 96 к. 3) 3 р. 24 к. 4) 36 р.

16. Седьмой класс писал контрольную работу по геометрии. В результате выяснилось, что 14 человек решили все 3 задачи контрольной работы, 11 человек решили 2 задачи, 5 человек — 1 задачу и 3 человека не решили ни одной задачи. Определите среднее число задач, решённых одним учеником.
1) \(\frac{11}{3}\) 2) \(2\) 3) \(2\frac{1}{11}\) 4) \(3\)

№ 1
\(0{,}44\), \(0{,}8\), \(\frac{2}{5}=0{,}4\), \(\frac{4}{9}=0{,}444\ldots\); наименьшее \(0{,}4\), значит ответ \(\frac{2}{5}\).

№ 2
Проверка вариантов: \(\frac{1}{16}>\frac{1}{15}\) — неверно; \(-\frac{1}{16}>-\frac{1}{15}\) — верно; \(-\frac{1}{15}>-\frac{1}{16}\) — неверно; \(-\frac{1}{15}>\frac{1}{16}\) — неверно. Ответ: при \(a=-16\), \(b=-15\).

№ 3
\(\frac{0{,}3\cdot 0{,}25}{0{,}45}=\frac{0{,}3\cdot 25}{45}=\frac{3\cdot 5}{9\cdot 10}=\frac{1}{6}\).

№ 4
\(\frac{2{,}37}{1{,}15\cdot 0{,}18}=2{,}37:(1{,}15\cdot 0{,}18)=(2{,}37:1{,}15):0{,}18\). Ответ: 1), 4).

№ 5
\(\frac{(a+x)(a-x)}{ax}=\frac{(-2+(-0{,}2))(-2-(-0{,}2))}{-2\cdot(-0{,}2)}=\frac{(-2{,}2)(-1{,}8)}{0{,}4}=\frac{3{,}96}{0{,}4}=9{,}9\).

№ 6
Неверно неравенство 4) \(-\frac{1}{a}<a\).

№ 7
\(7\cdot 7\cdot \ldots \cdot 7\) (10 множителей) \(\cdot\) \(5\cdot 5\cdot \ldots \cdot 5\) (20 множителей) \(=7^{10}\cdot 5^{20}\). Ответ: 1) \(7^{10}\cdot 5^{20}\).

№ 8
\(10\cdot(-0{,}3)^3=10\cdot(-0{,}027)=-0{,}27\).

№ 9
В порядке возрастания: \((-1{,}7)^3;\ -1{,}7;\ (-1{,}7)^2\). Ответ: 3).

№ 10
\(-(((-1)^{10}-(-1)^{11})^2)=-(1-(-1))^2=-(2)^2=-4\). Ответ: 1) \(-4\).

№ 11
\(\frac{3}{5}=0{,}6=60\%\), \(\frac{3}{10}=0{,}3=30\%\), \(0{,}07=7\%\), \(0{,}7=70\%\). Ответ: А2, Б4, В1, Г3.

№ 12
Если \(S_{AKLM}=100\%\), то \(S_{ABCD}=400\%\); \(400-100=300\%\). Ответ: на 300%.

№ 13
Если \(S_{ABCD}=100\%\), то \(S_{AKLM}=25\%\); \(100-25=75\%\). Ответ: на 75%.

№ 14
Всего \(10+40=50\) книг; доля для взрослых \(10:50\cdot 100\%=20\%\). Ответ: 3.

№ 15
После снижения на \(10\%\) стало \(90\%\): \(360:0{,}9=400\) к. \(=4\) р. Ответ: 1.

№ 16
Среднее \(=\frac{14\cdot 3+11\cdot 2+5\cdot 1+3\cdot 0}{14+11+5+3}=\frac{69}{33}=\frac{23}{11}=2\frac{1}{11}\). Ответ: 3) \(2\frac{1}{11}\) задачи.

№ 1
Сравним числа \(0{,}44\), \(0{,}8\), \(\frac{2}{5}\), \(\frac{4}{9}\), приведя обыкновенные дроби к десятичной записи. Для \(\frac{2}{5}\) делим \(2\) на \(5\): получаем \(0{,}4\), то есть \(\frac{2}{5}=0{,}4\). Для \(\frac{4}{9}\) деление \(4:9\) дает бесконечную периодическую дробь \(0{,}444\ldots\), то есть \(\frac{4}{9}=0{,}444\ldots\).

Теперь сравниваем: \(0{,}44\) и \(0{,}4\): по разрядам \(0{,}44>0{,}40\), значит \(0{,}44>0{,}4\). Также \(0{,}444\ldots>0{,}44\), потому что после \(0{,}44\) у периодической дроби дальше идут цифры \(4\). И \(0{,}8\) очевидно больше всех чисел около \(0{,}4\). Следовательно, наименьшее число \(0{,}4\), а это \(\frac{2}{5}\). Ответ: \(\frac{2}{5}\).

№ 2
Нужно выбрать такие \(a\) и \(b\), чтобы выполнялось \(\frac{1}{a}>\frac{1}{b}\). Проверяем каждый предложенный вариант подстановкой и сравниванием дробей, учитывая знак: при отрицательных знаменателях дроби тоже отрицательные, и сравнение меняется “наоборот” относительно модулей.

1) \(a=16\), \(b=15\): получаем \(\frac{1}{16}\) и \(\frac{1}{15}\). Так как \(\frac{1}{16}<\frac{1}{15}\), то \(\frac{1}{16}>\frac{1}{15}\) неверно.
2) \(a=-16\), \(b=-15\): \(\frac{1}{-16}=-\frac{1}{16}\), \(\frac{1}{-15}=-\frac{1}{15}\). Среди отрицательных чисел “больше” то, которое ближе к нулю: \(-\frac{1}{16}>-\frac{1}{15}\), потому что \(\frac{1}{16}<\frac{1}{15}\). Это верно.
3) \(a=-15\), \(b=-16\): получаем \(-\frac{1}{15}\) и \(-\frac{1}{16}\), но \(-\frac{1}{15}<-\frac{1}{16}\), значит условие неверно.
4) \(a=-15\), \(b=16\): \(-\frac{1}{15}\) и \(\frac{1}{16}\), отрицательное не больше положительного, условие неверно. Ответ: при \(a=-16\), \(b=-15\).

№ 3
Вычисляем \(\frac{0{,}3\cdot 0{,}25}{0{,}45}\). Удобно убрать десятичные дроби, заменив их обыкновенными: \(0{,}3=\frac{3}{10}\), \(0{,}25=\frac{25}{100}=\frac{1}{4}\), \(0{,}45=\frac{45}{100}=\frac{9}{20}\). Тогда выражение становится \(\frac{\frac{3}{10}\cdot \frac{1}{4}}{\frac{9}{20}}\).

Перемножаем в числителе: \(\frac{3}{10}\cdot \frac{1}{4}=\frac{3}{40}\). Деление на дробь заменяем умножением на обратную: \(\frac{3}{40}:\frac{9}{20}=\frac{3}{40}\cdot \frac{20}{9}\). Сокращаем \(20\) с \(40\): \(\frac{20}{40}=\frac{1}{2}\), получаем \(\frac{3}{2\cdot 9}=\frac{3}{18}=\frac{1}{6}\). Ответ: \(\frac{1}{6}\).

№ 4
Дано выражение вида \(\frac{2{,}37}{1{,}15\cdot 0{,}18}\). По записи видно, что в знаменателе стоит произведение \(1{,}15\cdot 0{,}18\), а все выражение — это деление \(2{,}37\) на это произведение. Поэтому эквивалентная запись через двоеточие: \(2{,}37:(1{,}15\cdot 0{,}18)\) — это вариант 1).

Также можно делить последовательно: сначала разделить \(2{,}37\) на \(1{,}15\), а результат разделить на \(0{,}18\). Это соответствует преобразованию \(\frac{2{,}37}{1{,}15\cdot 0{,}18}=\left(\frac{2{,}37}{1{,}15}\right):0{,}18\), то есть вариант 4) \((2{,}37:1{,}15):0{,}18\). Ответ: 1), 4).

№ 5
Подставляем \(a=-2\), \(x=-0{,}2\) в \(\frac{(a+x)(a-x)}{ax}\). Сначала находим \(a+x=-2+(-0{,}2)=-2{,}2\). Далее \(a-x=-2-(-0{,}2)=-2+0{,}2=-1{,}8\). Тогда числитель \((a+x)(a-x)=(-2{,}2)(-1{,}8)\).

Знаменатель \(ax=(-2)\cdot(-0{,}2)=0{,}4\). Перемножаем числитель: \((-2{,}2)(-1{,}8)=3{,}96\) (потому что \(22\cdot 18=396\) и две цифры после запятой). Делим: \(\frac{3{,}96}{0{,}4}=9{,}9\), так как деление на \(0{,}4\) эквивалентно умножению на \(\frac{10}{4}=2{,}5\): \(3{,}96\cdot 2{,}5=9{,}9\). Ответ: \(9{,}9\).

№ 6
По условию нужно указать, какое неравенство неверно; на фото отмечено: неверно неравенство 4) \(-\frac{1}{a}<a\). То есть именно вариант 4) не выполняется (при допустимых значениях \(a\), где выражение \(-\frac{1}{a}\) определено). Ответ: 4) \(-\frac{1}{a}<a\) — неверно.

№ 7
В произведении слева записано \(7\cdot 7\cdot 7\cdot \ldots \cdot 7\) (подписано \(10\) множителей) и затем \(5\cdot 5\cdot 5\cdot \ldots \cdot 5\) (подписано \(20\) множителей). По определению степени произведение одинаковых множителей записывается как степень: \(7\) повторяется \(10\) раз, значит это \(7^{10}\); \(5\) повторяется \(20\) раз, значит это \(5^{20}\).

Так как между этими группами стоит умножение, итоговое выражение равно произведению степеней: \(7^{10}\cdot 5^{20}\). Это совпадает с вариантом ответа на фото. Ответ: 1) \(7^{10}\cdot 5^{20}\).

№ 8
Нужно вычислить \(10\cdot (-0{,}3)^{3}\). Степень \(3\) означает тройное умножение: \((-0{,}3)^{3}=(-0{,}3)\cdot(-0{,}3)\cdot(-0{,}3)\). Сначала \((-0{,}3)\cdot(-0{,}3)=0{,}09\) (произведение двух отрицательных положительное), затем \(0{,}09\cdot(-0{,}3)=-0{,}027\) (произведение положительного на отрицательное отрицательное).

Теперь умножаем на \(10\): \(10\cdot(-0{,}027)=-0{,}27\), запятая сдвигается на один разряд вправо. Ответ: \(-0{,}27\).

№ 9
Нужно выбрать порядок возрастания для чисел \((-1{,}7)^{3}\), \(-1{,}7\), \((-1{,}7)^{2}\). Сначала оценим знаки и величины: \((-1{,}7)^{2}\) — квадрат отрицательного, значит положительное число \(2{,}89\). Число \(-1{,}7\) отрицательное. Куб \((-1{,}7)^{3}\) сохраняет отрицательный знак (нечетная степень), и по модулю больше, чем \(1{,}7\), потому что \(1{,}7^{3}=4{,}913\), значит \((-1{,}7)^{3}=-4{,}913\).

В порядке возрастания идут: самое маленькое \((-1{,}7)^{3}\) (самое “отрицательное”), затем \(-1{,}7\), затем положительное \((-1{,}7)^{2}\). На фото указан вариант 3) именно в таком порядке. Ответ: 3) \((-1{,}7)^{3};\ -1{,}7;\ (-1{,}7)^{2}\).

№ 10
Вычисляем \(-(((-1)^{10}-(-1)^{11})^{2})\). Сначала степени: \((-1)^{10}=1\), так как четная степень; \((-1)^{11}=-1\), так как нечетная степень. Тогда разность внутри скобок: \(1-(-1)=2\).

Далее возводим в квадрат: \(2^{2}=4\). Перед всем выражением стоит минус, значит \(-4\). На фото ответ: 1) \(-4\). Ответ: 1) \(-4\).

№ 11
Нужно сопоставить дроби/десятичные числа с процентами. Переводим в десятичные дроби и проценты (умножением на \(100\%\)). Для А: \(\frac{3}{5}=0{,}6\), значит \(60\%\). Для Б: \(\frac{3}{10}=0{,}3\), значит \(30\%\). Для В: \(0{,}07\) — это \(7\%\), потому что \(0{,}07\cdot 100\%=7\%\). Для Г: \(0{,}7\) — это \(70\%\).

Далее сверяем с нумерацией вариантов на фото: получается соответствие А2, Б4, В1, Г3. Ответ: А2, Б4, В1, Г3.

№ 12
Дано: квадрат \(AKLM\) составляет \(\frac{1}{4}\) квадрата \(ABCD\), то есть \(S_{AKLM}=\frac{1}{4}S_{ABCD}\). Чтобы сравнить “на сколько процентов” одна площадь больше другой, удобно принять меньшую за \(100\%\). Пусть \(S_{AKLM}=100\%\). Тогда из соотношения \(\frac{S_{AKLM}}{S_{ABCD}}=\frac{1}{4}\) получаем \(S_{ABCD}=400\%\).

Разность в процентах относительно \(AKLM\): \(400\%-100\%=300\%\). Значит площадь квадрата \(ABCD\) больше площади \(AKLM\) на \(300\%\). Ответ: на \(300\%\).

№ 13
Здесь то же соотношение \(S_{AKLM}=\frac{1}{4}S_{ABCD}\), но спрашивается, на сколько процентов \(AKLM\) меньше \(ABCD\). Удобно принять \(S_{ABCD}=100\%\). Тогда \(S_{AKLM}=\frac{1}{4}\cdot 100\%=25\%\).

Насколько меньше: \(100\%-25\%=75\%\). Это означает, что площадь \(AKLM\) меньше площади \(ABCD\) на \(75\%\). Ответ: на \(75\%\).

№ 14
По условию (как на фото) всего выпущено \(10+40=50\) книг. Чтобы найти долю книг для взрослых, берём отношение числа “взрослых” книг к общему числу: \(\frac{10}{50}\).

Переводим в проценты: \(\frac{10}{50}\cdot 100\%=\frac{1}{5}\cdot 100\%=0{,}2\cdot 100\%=20\%\). На фото выбран вариант ответа 3. Ответ: 3.

№ 15
Цена акции стала на \(10\%\) меньше, значит новая цена составляет \(100\%-10\%=90\%\) от первоначальной. По фото новая цена \(360\) к., то есть \(360\) к. — это \(90\%\) от старой цены. Тогда старая цена равна \(360:0{,}9\).

Вычисляем: \(360:0{,}9=400\) к. (деление на \(0{,}9\) увеличивает число), а \(400\) к. \(=4\) р. На фото указан вариант 1. Ответ: 1.

№ 16
Найдем среднее число решенных задач: суммарное количество задач делим на суммарное число учеников (по записи на фото это среднее, взвешенное по группам). Сумма решенных: \(14\cdot 3+11\cdot 2+5\cdot 1+3\cdot 0\). Это \(42+22+5+0=69\). Сумма учеников: \(14+11+5+3=33\).

Среднее \(=\frac{69}{33}\). Сокращаем на \(3\): \(\frac{69}{33}=\frac{23}{11}\). В смешанном виде \(\frac{23}{11}=2\frac{1}{11}\), потому что \(23=11\cdot 2+1\). На фото ответ: 3) \(2\frac{1}{11}\) задачи. Ответ: 3) \(2\frac{1}{11}\) задачи.