ГДЗ по Алгебре 7 Класс Номер 513 Дорофеев, Суворова — Подробные Ответы

Изобразите на координатной прямой множество точек, заданное неравенством:

a) \(|x — 20| < 5\);

б) \(|x — 6| > 1\);

в) \(|x + 1,5| < 5\);

г) \(|x + 0,5| > 2,5\).

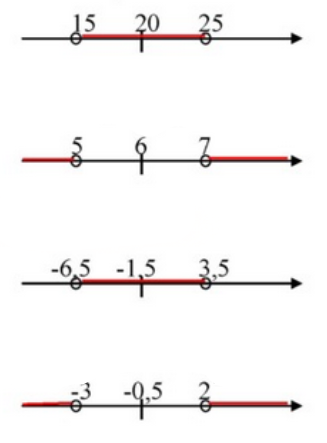
а) Неравенство \(|x — 20| < 5\) означает, что расстояние от \(x\) до 20 меньше 5. Значит, \(x\) лежит между 15 и 25: \(15 < x < 25\).

б) Неравенство \(|x — 6| > 1\) означает, что расстояние от \(x\) до 6 больше 1. Значит, \(x\) лежит вне интервала от 5 до 7: \(x < 5\) или \(x > 7\).

в) Неравенство \(|x + 1,5| < 5\) означает, что расстояние от \(x\) до \(-1,5\) меньше 5. Значит, \(x\) лежит между \(-6,5\) и \(3,5\): \(-6,5 < x < 3,5\).

г) Неравенство \(|x + 0,5| > 2,5\) означает, что расстояние от \(x\) до \(-0,5\) больше 2,5. Значит, \(x\) лежит вне интервала от \(-3\) до \(2\): \(x < -3\) или \(x > 2\).

а) Неравенство \(|x — 20| < 5\) означает, что расстояние между числом \(x\) и числом 20 на числовой оси меньше 5. Геометрически это означает, что \(x\) находится внутри интервала, центр которого равен 20, а длина интервала равна 10 (по 5 в обе стороны от центра). Чтобы найти этот интервал, нужно решить двойное неравенство: \( -5 < x — 20 < 5 \). Прибавляя 20 ко всем частям неравенства, получаем \(15 < x < 25\). Таким образом, множество решений — все точки на числовой оси между 15 и 25, не включая сами концы.

б) Неравенство \(|x — 6| > 1\) означает, что расстояние между числом \(x\) и числом 6 больше 1. Это значит, что \(x\) лежит вне интервала длиной 2, центрированного в точке 6. Чтобы найти это множество, решаем двойное неравенство: \(x — 6 > 1\) или \(x — 6 < -1\). Из первого следует \(x > 7\), из второго — \(x < 5\). Значит, решения — это объединение двух промежутков: все числа меньше 5 и все числа больше 7. Сам интервал от 5 до 7 не включается, так как там расстояние до 6 меньше или равно 1.

в) Неравенство \(|x + 1,5| < 5\) означает, что расстояние между числом \(x\) и числом \(-1,5\) меньше 5. Это значит, что \(x\) лежит внутри интервала длиной 10, центрированного в точке \(-1,5\). Решаем двойное неравенство: \(-5 < x + 1,5 < 5\). Вычитаем 1,5 из всех частей: \(-6,5 < x < 3,5\). Следовательно, множество решений — все точки на числовой оси между \(-6,5\) и \(3,5\), не включая концы.

г) Неравенство \(|x + 0,5| > 2,5\) означает, что расстояние между числом \(x\) и числом \(-0,5\) больше 2,5. Это значит, что \(x\) лежит вне интервала длиной 5, центрированного в точке \(-0,5\). Решаем двойное неравенство: \(x + 0,5 > 2,5\) или \(x + 0,5 < -2,5\). Из первого получаем \(x > 2\), из второго — \(x < -3\). Значит, решения — объединение двух промежутков: все числа меньше \(-3\) и все числа больше 2. Интервал от \(-3\) до 2 не включается, так как там расстояние до \(-0,5\) меньше или равно 2,5.