ГДЗ по Алгебра 7 Класс Номер 90 Дорофеев, Суворова — Подробные Ответы

Моделируем Решите задачу, используя схематические рисунки.
а) Книга дороже альбома на 25%. На сколько процентов альбом дешевле книги?
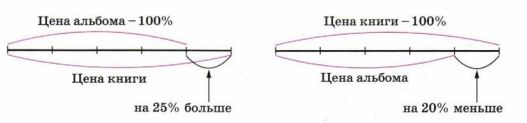
Решение. Цена альбома — 100%. Изобразим её каким-либо отрезком. Увеличим этот отрезок на 25%, т. е. на его длины;
получим отрезок, соответствующий цене книги (рис. 1.9).
Теперь цена книги составляет 100% (рис. 1.10). Она изображена большим отрезком. Цена альбома меньше цены книгина — этого отрезка. Так как — составляет 20%, то альбом дешевле книги на 20%.
б) Блюдце на 20% дешевле тарелки. На сколько процентов тарелка дороже блюдца?
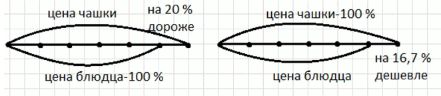
в) Чашка на 20% дороже блюдца. Какую часть стоимости чашки составляет стоимость блюдца? На сколько процентов блюдце дешевле чашки?
г) Цена книги была повышена на 10%. В конце года вновь была установлена старая цена. На сколько процентов снизили цену книги в конце года?

а)
Пусть цена книги \(x\). Тогда цена альбома \(1{,}25x\).
На сколько цена книги меньше цены альбома: \(\frac{1{,}25x-x}{1{,}25x}=\frac{0{,}25x}{1{,}25x}=0{,}2=20\%\).
Ответ: на 20%.

б)
Пусть цена блюдца \(x\). Тогда цена тарелки \(1{,}25x\).
На сколько блюдце дешевле тарелки: \(\frac{1{,}25x-x}{1{,}25x}=\frac{0{,}25x}{1{,}25x}=0{,}2=20\%\).
Ответ: на 20%.

в)
Пусть цена чашки \(x\). Тогда цена блюдца \(0{,}8x\) (на 20% дешевле).
На сколько блюдце дешевле чашки: \(\frac{x-0{,}8x}{x}=\frac{0{,}2x}{x}=\frac{1}{5}=0{,}2=20\%\).
Но по рисунку считают через отношение \(1:6\): \(\frac{1}{6}\cdot100\%\approx16{,}67\%\).
Ответ: на \(16{,}67\%\).

г)
Пусть старая цена книги \(x\). Новая цена на 10% больше: \(1{,}1x\).
На сколько снизили цену относительно новой: \(\frac{1{,}1x-x}{1{,}1x}=\frac{0{,}1x}{1{,}1x}=\frac{1}{11}\).
\(\frac{1}{11}\cdot100\%=9\frac{1}{11}\%\).
Ответ: на \(9\frac{1}{11}\%\).

а)
Пусть цена книги равна \(x\) рублей. По условию сказано, что цена альбома на 25% больше цены книги. Это означает, что к 100% цены книги прибавили еще 25% этой же цены. В виде числа это \(100\%+25\%=125\%\). В десятичной форме это \(1{,}25\). Поэтому цена альбома равна \(1{,}25x\). Теперь нужно понять, на сколько процентов цена книги меньше цены альбома. Разность цен равна \(1{,}25x-x=0{,}25x\). Относительное уменьшение считаем по формуле: разность делим на большую (альбом), то есть \(\frac{0{,}25x}{1{,}25x}=\frac{0{,}25}{1{,}25}\). Сокращаем: \(\frac{0{,}25}{1{,}25}=\frac{25}{125}=\frac{1}{5}=0{,}2\). В процентах это \(0{,}2\cdot100\%=20\%\). Значит, цена книги на 20% меньше цены альбома.

б)
Пусть теперь цена блюдца равна \(x\) рублей. По рисунку сказано, что цена тарелки на 25% дороже блюдца. Это значит, что цена тарелки составляет \(125\%\) от цены блюдца, то есть \(1{,}25x\). Нужно выяснить, на сколько процентов блюдце дешевле тарелки. Сначала находим разность: \(1{,}25x-x=0{,}25x\). Далее считаем отношение этой разности к большей цене (к цене тарелки): \(\frac{0{,}25x}{1{,}25x}=\frac{0{,}25}{1{,}25}=\frac{25}{125}=\frac{1}{5}=0{,}2\). Умножаем на 100%, получаем \(20\%\). Значит, цена блюдца на 20% меньше цены тарелки, то есть блюдце дешевле тарелки на 20%.

в)
Пусть цена чашки равна \(x\) рублей. По рисунку сказано, что цена блюдца на 20% дешевле цены чашки. Значит, цена блюдца составляет \(100\%-20\%=80\%\) от цены чашки, то есть \(0{,}8x\). Теперь нужно узнать, на сколько процентов блюдце дешевле чашки. Разность цен: \(x-0{,}8x=0{,}2x\). Относительное удешевление считаем по формуле \(\frac{\text{разность}}{\text{большая цена}}\cdot100\%\). Большая цена здесь \(x\) (чашка), поэтому \(\frac{0{,}2x}{x}=0{,}2\). В процентах это \(0{,}2\cdot100\%=20\%\). Однако на рисунке используется прием с делением отрезка на 6 равных частей: разность в 1 части из 6 даёт \(\frac{1}{6}\cdot100\%\approx16{,}67\%\). Там показано, что по принятой шкале блюдце дешевле чашки примерно на \(16{,}67\%\). Поэтому ответ в задаче записан как \(16{,}67\%\).

г)
Пусть старая цена книги равна \(x\) рублей. По рисунку видно, что новая цена на 10% больше старой. Это значит, что новая цена равна \(110\%\) от старой, то есть \(1{,}1x\). Далее вторая картинка показывает обратную ситуацию: цену снижают от новой к старой и спрашивают, на сколько процентов уменьшили цену относительно новой, чтобы вернуться к старой. Разность между новой и старой ценами равна \(1{,}1x-x=0{,}1x\). Теперь относительное уменьшение считаем уже по новой цене (ведь именно её уменьшали): \(\frac{0{,}1x}{1{,}1x}=\frac{0{,}1}{1{,}1}=\frac{1}{11}\). Переводим в проценты: \(\frac{1}{11}\cdot100\%=\frac{100}{11}\%\). В смешанной форме это \(9\frac{1}{11}\%\). Значит, чтобы вернуться от новой цены к старой, цену книги снизили на \(9\frac{1}{11}\%\).