ГДЗ по Алгебре 7 Класс Номер 765 Дорофеев, Суворова — Подробные Ответы

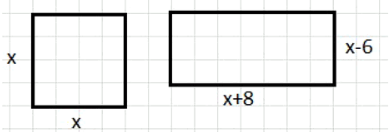
а) Пекарня использует для выпечки тортов формы двух видов, имеющие одинаковую площадь дна. У одной из них дно квадратное, а у другой — прямоугольное. Длина прямоугольной формы на 8 см больше, а ширина на 6 см меньше, чем сторона квадратной формы. Найдите размеры дна каждой формы.

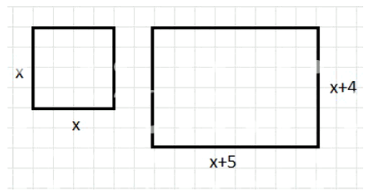
б) Под строительство был отведён участок земли, имеющий форму квадрата. Площадь этого участка пришлось увеличить на 830 м². Для этого одну из сторон первоначального участка увеличили на 4 м, а другую — на 5 м и получили новый участок прямоугольной формы. Чему была равна площадь первоначального участка?

а) Сделаем уравнение: \( x^2 = (x — 6)(x + 8) \).

Раскроем скобки: \( x^2 = x^2 + 8x — 6x — 48 \).

Сократим: \( 0 = 2x — 48 \), значит \( 2x = 48 \).

Получаем \( x = 24 \) (см).

Ширина прямоугольной формы: \( x — 6 = 24 — 6 = 18 \) (см).

Длина прямоугольной формы: \( x + 8 = 24 + 8 = 32 \) (см).

Ответ: 24 см; 18 см и 32 см.

б) Сделаем уравнение: \( (x + 4)(x + 5) — x^2 = 830 \).

Раскроем скобки: \( x^2 + 5x + 4x + 20 — x^2 = 830 \).

Сократим: \( 9x + 20 = 830 \), значит \( 9x = 810 \).

Получаем \( x = 90 \) (м).

Площадь первоначального участка: \( x^2 = 90^2 = 8100 \) (м²).

Ответ: 8100 м².

а) Пусть сторона квадратной формы равна \( x \) сантиметров. Тогда площадь квадратной формы равна \( x^{2} \). Прямоугольная форма имеет длину на 8 сантиметров больше, то есть \( x + 8 \), и ширину на 6 сантиметров меньше, то есть \( x — 6 \). Площадь прямоугольной формы равна произведению длины на ширину, то есть \( (x + 8)(x — 6) \).

Так как площади форм равны, составляем уравнение: \( x^{2} = (x + 8)(x — 6) \). Раскроем скобки в правой части: \( x^{2} = x^{2} + 8x — 6x — 48 \). Упростим выражение: \( x^{2} = x^{2} + 2x — 48 \). Переносим все в левую часть: \( x^{2} — x^{2} = 2x — 48 \), что упрощается до \( 0 = 2x — 48 \).

Решаем уравнение: \( 2x = 48 \), откуда \( x = 24 \) сантиметра. Это сторона квадратной формы. Далее находим размеры прямоугольной формы: ширина \( x — 6 = 24 — 6 = 18 \) сантиметров, длина \( x + 8 = 24 + 8 = 32 \) сантиметра. Ответ: сторона квадратной формы 24 см, прямоугольной формы — 18 см на 32 см.

б) Пусть сторона первоначального квадратного участка равна \( x \) метров, тогда площадь равна \( x^{2} \) квадратных метров. После увеличения участка одна сторона стала \( x + 4 \) метров, другая — \( x + 5 \) метров. Площадь нового участка равна произведению этих сторон, то есть \( (x + 4)(x + 5) \).

По условию площадь увеличилась на 830 м², значит разность площадей равна 830: \( (x + 4)(x + 5) — x^{2} = 830 \). Раскроем скобки: \( x^{2} + 5x + 4x + 20 — x^{2} = 830 \). Упростим: \( 9x + 20 = 830 \). Переносим 20 в правую часть: \( 9x = 830 — 20 \), то есть \( 9x = 810 \).

Решаем уравнение: \( x = \frac{810}{9} = 90 \) метров — сторона первоначального квадратного участка. Площадь первоначального участка равна \( x^{2} = 90^{2} = 8100 \) квадратных метров. Ответ: площадь первоначального участка была 8100 м².