ГДЗ по Алгебре 7 Класс Номер 764 Дорофеев, Суворова — Подробные Ответы

Решите задачу:

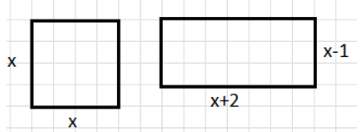
а) Площадь квадрата равна площади прямоугольника, одна из сторон которого на 1 см меньше стороны квадрата, а другая на 2 см больше стороны квадрата. Найдите длину стороны квадрата и длины сторон прямоугольника.

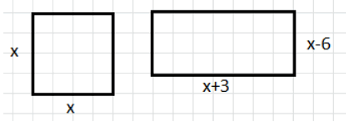
б) Площадь квадрата на 63 см² больше площади прямоугольника. Одна из сторон прямоугольника на 3 см больше, а другая на 6 см меньше стороны квадрата. Найдите площадь квадрата.

а) Составим уравнение: \( x^2 = (x — 1)(x + 2) \).

Раскроем скобки: \( x^2 = x^2 + 2x — x — 2 \).

Сократим: \( 0 = x — 2 \).

Получаем: \( x = 2 \) см — сторона квадрата.

Ширина прямоугольника: \( x — 1 = 2 — 1 = 1 \) см.

Длина прямоугольника: \( x + 2 = 2 + 2 = 4 \) см.

Ответ: 2 см; 1 см и 4 см.

б) Составим уравнение: \( x^2 — (x — 6)(x + 3) = 63 \).

Раскроем скобки: \( x^2 — (x^2 + 3x — 6x — 18) = 63 \).

Упростим: \( x^2 — x^2 — 3x + 6x + 18 = 63 \).

Получим: \( 3x + 18 = 63 \).

Вычислим: \( 3x = 45 \), \( x = 15 \) см — сторона квадрата.

Площадь квадрата: \( x^2 = 15^2 = 225 \) см².

Ответ: 225 см².

а) Пусть сторона квадрата равна \( x \) сантиметрам. Тогда площадь квадрата будет равна \( x^{2} \). По условию, площадь прямоугольника равна площади квадрата. Известно, что одна сторона прямоугольника на 1 сантиметр меньше стороны квадрата, то есть равна \( x — 1 \), а другая сторона на 2 сантиметра больше стороны квадрата, то есть равна \( x + 2 \). Площадь прямоугольника равна произведению его сторон, значит она равна \( (x — 1)(x + 2) \).

Для нахождения значения \( x \) составим уравнение равенства площадей: \( x^{2} = (x — 1)(x + 2) \). Раскроем скобки справа: \( (x — 1)(x + 2) = x^{2} + 2x — x — 2 = x^{2} + x — 2 \). Подставим это в уравнение: \( x^{2} = x^{2} + x — 2 \). Чтобы упростить уравнение, вычтем \( x^{2} \) с обеих сторон: \( 0 = x — 2 \).

Отсюда следует, что \( x = 2 \). Это и есть длина стороны квадрата. Теперь найдём стороны прямоугольника: первая сторона равна \( x — 1 = 2 — 1 = 1 \) сантиметр, вторая сторона равна \( x + 2 = 2 + 2 = 4 \) сантиметра. Таким образом, сторона квадрата равна 2 сантиметрам, а стороны прямоугольника — 1 и 4 сантиметрам соответственно.

б) Пусть сторона квадрата равна \( x \) сантиметрам. Тогда площадь квадрата равна \( x^{2} \). По условию, площадь квадрата на 63 квадратных сантиметра больше площади прямоугольника. Прямоугольник имеет стороны, одна из которых на 6 сантиметров меньше стороны квадрата, то есть \( x — 6 \), а другая на 3 сантиметра больше стороны квадрата, то есть \( x + 3 \). Площадь прямоугольника равна произведению этих сторон: \( (x — 6)(x + 3) \).

Составим уравнение, выражающее разницу площадей: \( x^{2} — (x — 6)(x + 3) = 63 \). Раскроем скобки: \( (x — 6)(x + 3) = x^{2} + 3x — 6x — 18 = x^{2} — 3x — 18 \). Подставим в уравнение: \( x^{2} — (x^{2} — 3x — 18) = 63 \). Раскроем скобки с минусом: \( x^{2} — x^{2} + 3x + 18 = 63 \), что упрощается до \( 3x + 18 = 63 \).

Вычтем 18 с обеих сторон: \( 3x = 45 \). Разделим обе части на 3: \( x = 15 \). Это длина стороны квадрата. Площадь квадрата равна \( x^{2} = 15^{2} = 225 \) квадратных сантиметров. Таким образом, площадь квадрата равна 225 см^{2}.