ГДЗ по Алгебре 7 Класс Номер 760 Дорофеев, Суворова — Подробные Ответы

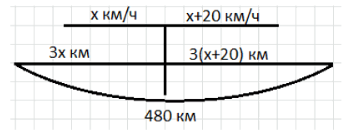
а) Два поезда, встретившись на разъезде, продолжали движение каждый в своём направлении. Скорость одного из них на 20 км/ч больше скорости другого. Через 3 ч расстояние между ними было 480 км. Найдите скорость каждого поезда.

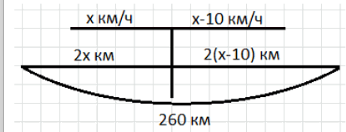
б) Два автомобиля едут по шоссе навстречу друг другу. Скорость одного из них на 10 км/ч меньше скорости другого. Через 2 ч после того, как они встретились, расстояние между ними стало равным 260 км. Найдите скорость каждого автомобиля.

а) Сделаем рисунок:

\(3x + 3(x+20) = 480\)

\(3x + 3x + 60 = 480\)

\(6x = 480 — 60\)

\(6x = 420\)

\(x = 70\) (км/ч) – скорость первого поезда.

\(x + 20 = 70 + 20 = 90\) (км/ч) – скорость второго поезда.

Ответ: 70 км/ч и 90 км/ч.

б) Сделаем рисунок:

\(2x + 2(x — 10) = 260\)

\(2x + 2x — 20 = 260\)

\(4x = 260 + 20\)

\(4x = 280\)

\(x = 70\) (км/ч) – скорость первого автомобиля.

\(x — 10 = 70 — 10 = 60\) (км/ч) – скорость второго автомобиля.

Ответ: 70 км/ч и 60 км/ч.

а) Рассмотрим первый случай с двумя поездами, которые движутся в противоположных направлениях после встречи. Пусть скорость первого поезда равна \( x \) км/ч. Тогда скорость второго поезда будет на 20 км/ч больше, то есть \( x + 20 \) км/ч. За 3 часа каждый поезд проедет расстояние, равное произведению своей скорости на время: первый — \( 3x \) км, второй — \( 3(x + 20) \) км. Поскольку поезда удаляются друг от друга, сумма этих расстояний равна 480 км. Составим уравнение: \( 3x + 3(x + 20) = 480 \).

Раскроем скобки и упростим уравнение: \( 3x + 3x + 60 = 480 \), что приводит к \( 6x + 60 = 480 \). Вычтем 60 из обеих частей: \( 6x = 480 — 60 \), то есть \( 6x = 420 \). Разделим обе части на 6: \( x = \frac{420}{6} = 70 \). Таким образом, скорость первого поезда равна 70 км/ч. Скорость второго поезда будет \( 70 + 20 = 90 \) км/ч.

Ответ: скорость первого поезда 70 км/ч, второго — 90 км/ч.

б) Во втором случае два автомобиля движутся навстречу друг другу и после встречи расстояние между ними через 2 часа становится 260 км. Пусть скорость первого автомобиля равна \( x \) км/ч. Тогда скорость второго автомобиля на 10 км/ч меньше, то есть \( x — 10 \) км/ч. За 2 часа первый автомобиль проедет \( 2x \) км, второй — \( 2(x — 10) \) км. Сумма пройденных ими расстояний равна 260 км, поэтому составляем уравнение: \( 2x + 2(x — 10) = 260 \).

Раскроем скобки и упростим: \( 2x + 2x — 20 = 260 \), что даёт \( 4x — 20 = 260 \). Прибавим 20 к обеим частям: \( 4x = 260 + 20 \), то есть \( 4x = 280 \). Разделим обе части на 4: \( x = \frac{280}{4} = 70 \). Следовательно, скорость первого автомобиля равна 70 км/ч, а второго — \( 70 — 10 = 60 \) км/ч.

Ответ: скорость первого автомобиля 70 км/ч, второго — 60 км/ч.