ГДЗ по Алгебре 7 Класс Номер 759 Дорофеев, Суворова — Подробные Ответы

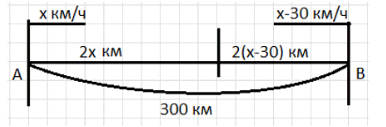
а) Расстояние между двумя железнодорожными станциями А и В равно 300 км. От станции А по направлению к станции В вышел пассажирский поезд. Одновременно навстречу ему от станции В вышел электропоезд, скорость которого на 30 км/ч меньше скорости пассажирского поезда. Они встретились через 2 ч на разъезде. На каком расстоянии от А и от В находится разъезд?

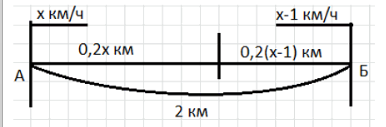
б) Расстояние между домами Андрея и Бориса, расположенными на одном шоссе, 2 км. Они выходят одновременно из своих домов навстречу друг другу и встречаются через 0,2 ч. Скорость Андрея на 1 км/ч больше скорости Бориса. На каком расстоянии от дома Бориса произошла встреча?

Подсказка. Задачу легче решить, если обозначить буквой какую-нибудь из скоростей.

а) Пусть \( x \) — скорость пассажирского поезда. Тогда скорость электропоезда \( x — 30 \). За 2 часа пассажирский поезд проедет \( 2x \), электропоезд — \( 2(x — 30) \). Составляем уравнение: \( 2x + 2(x — 30) = 300 \). Раскрываем скобки: \( 2x + 2x — 60 = 300 \). Суммируем: \( 4x = 360 \). Находим \( x = 90 \) км/ч. Расстояние от \( A \): \( 2 \cdot 90 = 180 \) км, от \( B \): \( 300 — 180 = 120 \) км. Ответ: 180 км от \( A \), 120 км от \( B \).

б) Пусть скорость Бориса \( x — 1 \), Андрея — \( x \). За 0,2 часа Андрей пройдет \( 0,2x \), Борис — \( 0,2(x — 1) \). Составляем уравнение: \( 0,2x + 0,2(x — 1) = 2 \). Раскрываем: \( 0,2x + 0,2x — 0,2 = 2 \). Суммируем: \( 0,4x = 2,2 \). Находим \( x = \frac{22}{4} = 5,5 \) км/ч. Скорость Бориса \( 5,5 — 1 = 4,5 \) км/ч. Расстояние от дома Бориса: \( 0,2 \cdot 4,5 = 0,9 \) км. Ответ: 0,9 км.

а) Пусть \( x \) — скорость пассажирского поезда в километрах в час. Тогда скорость электропоезда будет на 30 км/ч меньше, то есть \( x — 30 \). По условию, поезда встретились через 2 часа, значит, за это время каждый из них проехал определённое расстояние. Пассажирский поезд за 2 часа проедет путь \( 2x \), а электропоезд — путь \( 2(x — 30) \). Сумма этих двух расстояний равна общему расстоянию между станциями \( A \) и \( B \), которое равно 300 км. Поэтому составляем уравнение: \( 2x + 2(x — 30) = 300 \).

Раскроем скобки и упростим уравнение: \( 2x + 2x — 60 = 300 \). Сложим похожие члены: \( 4x — 60 = 300 \). Чтобы найти \( x \), перенесём \( -60 \) вправо, поменяв знак: \( 4x = 300 + 60 \), то есть \( 4x = 360 \). Разделим обе части уравнения на 4: \( x = \frac{360}{4} = 90 \). Таким образом, скорость пассажирского поезда равна 90 км/ч.

Теперь найдём расстояния от станций до разъезда, где они встретились. Пассажирский поезд проехал \( 2x = 2 \times 90 = 180 \) км, то есть разъезд находится в 180 км от станции \( A \). Электропоезд проехал оставшееся расстояние: \( 300 — 180 = 120 \) км, значит, разъезд находится в 120 км от станции \( B \). Ответ: 180 км от \( A \), 120 км от \( B \).

б) Пусть скорость Бориса равна \( x — 1 \) км/ч, тогда скорость Андрея — \( x \) км/ч. Они выходят одновременно навстречу друг другу и встречаются через 0,2 часа. За это время Андрей проедет путь \( 0,2x \), а Борис — путь \( 0,2(x — 1) \). Сумма этих расстояний равна расстоянию между домами, то есть 2 км. Составим уравнение: \( 0,2x + 0,2(x — 1) = 2 \).

Раскроем скобки: \( 0,2x + 0,2x — 0,2 = 2 \). Сложим похожие члены: \( 0,4x — 0,2 = 2 \). Переносим \( -0,2 \) вправо, меняя знак: \( 0,4x = 2 + 0,2 \), то есть \( 0,4x = 2,2 \). Разделим обе части уравнения на 0,4: \( x = \frac{2,2}{0,4} = \frac{22}{4} = 5,5 \). Значит, скорость Андрея равна 5,5 км/ч.

Скорость Бориса равна \( x — 1 = 5,5 — 1 = 4,5 \) км/ч. Теперь найдём, на каком расстоянии от дома Бориса произошла встреча. Борис за 0,2 часа проезжает путь \( 0,2 \times 4,5 = 0,9 \) км. Ответ: встреча произошла в 0,9 км от дома Бориса.