ГДЗ по Алгебре 7 Класс Номер 758 Дорофеев, Суворова — Подробные Ответы

а) Турист вышел из пункта А по направлению к пункту В, расстояние до которого равно 9 км. Одновременно с ним из пункта В в пункт А выехал велосипедист, скорость которого на 10 км/ч больше скорости туриста. Через 0,5 ч они встретились. Определите скорость, с которой шёл турист.

б) Два мальчика выбегают одновременно навстречу друг другу из двух точек, расстояние между которыми 660 м, и встречаются через 2 мин. Один из них пробегает на 30 м в минуту меньше, чем другой. Сколько метров в минуту пробегает каждый из них?

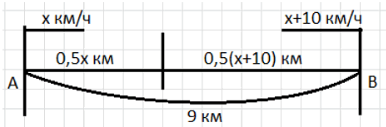
а) Сделаем рисунок:
Пусть скорость туриста \( x \) км/ч, скорость велосипедиста \( x + 10 \) км/ч.
За 0,5 часа турист прошёл \( 0{,}5x \) км, велосипедист — \( 0{,}5(x + 10) \) км.
Составим уравнение:
\( 0{,}5x + 0{,}5(x + 10) = 9 \)
Раскроем скобки:
\( 0{,}5x + 0{,}5x + 5 = 9 \)
Сложим:
\( x + 5 = 9 \)
Вычислим:
\( x = 9 — 5 = 4 \) км/ч — скорость туриста.
Ответ: 4 км/ч.

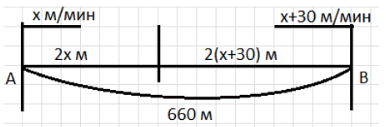
б) Сделаем рисунок:
Пусть скорость первого мальчика \( x \) м/мин, второго — \( x + 30 \) м/мин.
За 2 минуты первый пробежит \( 2x \) м, второй — \( 2(x + 30) \) м.
Составим уравнение:
\( 2x + 2(x + 30) = 660 \)
Раскроем скобки:
\( 2x + 2x + 60 = 660 \)
Сложим:
\( 4x + 60 = 660 \)
Вычислим:
\( 4x = 660 — 60 = 600 \)
\( x = \frac{600}{4} = 150 \) м/мин — скорость первого мальчика.
Скорость второго:
\( x + 30 = 150 + 30 = 180 \) м/мин.
Ответ: 150 м/мин и 180 м/мин.

а) Рассмотрим ситуацию, когда турист и велосипедист движутся навстречу друг другу с разными скоростями. Пусть скорость туриста равна \( x \) км/ч, тогда скорость велосипедиста на 10 км/ч больше, то есть \( x + 10 \) км/ч. Они встретились через 0,5 часа, значит за это время каждый прошёл определённое расстояние. Турист за 0,5 часа преодолел путь длиной \( 0{,}5x \) км, а велосипедист — \( 0{,}5(x + 10) \) км. Сумма этих расстояний равна общему расстоянию между пунктами А и В, которое равно 9 км.

Составим уравнение, отражающее эту зависимость: \( 0{,}5x + 0{,}5(x + 10) = 9 \). Раскроем скобки: \( 0{,}5x + 0{,}5x + 5 = 9 \). Далее сложим подобные слагаемые: \( x + 5 = 9 \). Чтобы найти скорость туриста, нужно из 9 вычесть 5, получаем \( x = 4 \). Это означает, что турист движется со скоростью 4 км/ч.

Таким образом, скорость туриста равна 4 км/ч. Эта величина логична, так как велосипедист быстрее туриста на 10 км/ч, и за 0,5 часа они вместе преодолевают 9 км. Если турист идёт медленнее, а велосипедист быстрее, то их суммарное расстояние за полчаса совпадает с расстоянием между пунктами.

б) В задаче с двумя мальчиками расстояние между ними составляет 660 метров. Они бегут навстречу друг другу и встречаются через 2 минуты. Пусть скорость первого мальчика равна \( x \) м/мин, тогда скорость второго мальчика на 30 м/мин больше, то есть \( x + 30 \) м/мин. За 2 минуты первый мальчик пробежит \( 2x \) метров, а второй — \( 2(x + 30) \) метров. Сумма этих расстояний равна общему расстоянию между ними — 660 метров.

Составим уравнение: \( 2x + 2(x + 30) = 660 \). Раскроем скобки: \( 2x + 2x + 60 = 660 \). Сложим подобные слагаемые: \( 4x + 60 = 660 \). Чтобы найти \( x \), нужно из 660 вычесть 60, получается \( 4x = 600 \). Разделим обе части уравнения на 4: \( x = \frac{600}{4} = 150 \). Это скорость первого мальчика — 150 м/мин.

Теперь найдём скорость второго мальчика, прибавив 30 к скорости первого: \( 150 + 30 = 180 \) м/мин. Таким образом, первый мальчик бежит со скоростью 150 м/мин, а второй — 180 м/мин. Эти значения соответствуют условию задачи, поскольку за 2 минуты они вместе преодолевают 660 метров, бегут навстречу друг другу, а разница в скоростях составляет 30 м/мин.