ГДЗ по Алгебре 7 Класс Номер 741 Дорофеев, Суворова — Подробные Ответы

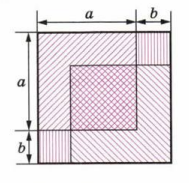
Докажите, что \((a + b)^2 + (a — b)^2 = 2(a^2 + b^2).\) Поясните это равенство с помощью рисунка 7.9.

\((a + b)^2 + (a — b)^2 = (a^2 + 2ab + b^2) + (a^2 — 2ab + b^2)\)

\(= a^2 + 2ab + b^2 + a^2 — 2ab + b^2\)

\(= 2a^2 + 2b^2 = 2(a^2 + b^2)\)

\((a + b)^2\) — площадь большого квадрата

\((a — b)^2\) — площадь малого квадрата

\(a^2\) — площадь квадрата со стороной \(a\)

\(b^2\) — площадь квадрата со стороной \(b\)

\(2(a^2 + b^2) = (a + b)^2 + (a — b)^2\) — сумма площадей большого и малого квадратов равна удвоенной сумме площадей квадратов со сторонами \(a\) и \(b\)

Рассмотрим выражение \((a + b)^2 + (a — b)^2\). Для начала раскроем скобки каждого слагаемого, используя формулу квадрата суммы и квадрата разности. По формуле, \((a + b)^2 = a^2 + 2ab + b^2\), а \((a — b)^2 = a^2 — 2ab + b^2\). Это базовые алгебраические тождества, которые позволяют представить квадрат суммы и разности в виде суммы квадратов и удвоенного произведения.

Теперь сложим полученные выражения: \((a + b)^2 + (a — b)^2 = (a^2 + 2ab + b^2) + (a^2 — 2ab + b^2)\). При сложении необходимо сложить все подобные члены. Обратим внимание, что \(+2ab\) и \(-2ab\) взаимно уничтожаются, так как они противоположны по знаку. В итоге остается сумма \(a^2 + a^2 + b^2 + b^2\), что равно \(2a^2 + 2b^2\).

Таким образом, итоговое выражение можно записать как \(2(a^2 + b^2)\). Это доказывает равенство \((a + b)^2 + (a — b)^2 = 2(a^2 + b^2)\). Геометрически это означает, что сумма площадей двух квадратов со сторонами \(a + b\) и \(a — b\) равна удвоенной сумме площадей квадратов со сторонами \(a\) и \(b\). Здесь \((a + b)^2\) — площадь большого квадрата, \((a — b)^2\) — площадь меньшего квадрата, \(a^2\) и \(b^2\) — площади квадратов с соответствующими сторонами. Такое равенство помогает понять взаимосвязь между площадями фигур и алгебраическими выражениями.