ГДЗ по Алгебре 7 Класс Номер 740 Дорофеев, Суворова — Подробные Ответы

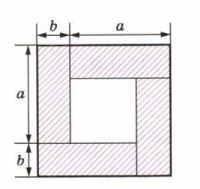
Докажите, что \((a + b)^2 — (a — b)^2 = 4ab.\) Поясните это равенство с помощью рисунка 7.8.

\((a+b)^2 — (a-b)^2 = a^2 + 2ab + b^2 — (a^2 — 2ab + b^2) =\)
\(= a^2 + 2ab + b^2 — a^2 + 2ab — b^2 = 4ab\)

\((a+b)^2 — (a-b)^2 = 4ab\) утверждение доказано

\((a+b)^2\) — площадь большого квадрата

\((a-b)^2\) — площадь малого квадрата

\(ab\) — площадь одного прямоугольника

\(4ab\) — сумма площадей четырех прямоугольников

\((a+b)^2 — (a-b)^2 = 4ab\) утверждение доказано

Рассмотрим выражение \((a + b)^2 — (a — b)^2\). Чтобы упростить его, раскроем скобки, используя формулы квадрата суммы и квадрата разности. По формуле, \((a + b)^2 = a^2 + 2ab + b^2\), а \((a — b)^2 = a^2 — 2ab + b^2\). Теперь подставим эти выражения в исходное: \((a + b)^2 — (a — b)^2 = (a^2 + 2ab + b^2) — (a^2 — 2ab + b^2)\).

Выполним вычитание, раскрывая скобки: \(a^2 + 2ab + b^2 — a^2 + 2ab — b^2\). Здесь можно сократить одинаковые слагаемые: \(a^2 — a^2 = 0\) и \(b^2 — b^2 = 0\), поэтому остаётся только \(2ab + 2ab = 4ab\). Таким образом, алгебраически доказано, что \((a + b)^2 — (a — b)^2 = 4ab\).

Геометрически это равенство можно объяснить с помощью представления площадей. Квадрат со стороной \(a + b\) имеет площадь \((a + b)^2\), а квадрат со стороной \(a — b\) — площадь \((a — b)^2\). Разность этих площадей — это площадь кольцевой области, которая состоит из четырёх прямоугольников, каждый из которых имеет площадь \(ab\). Значит, суммарная площадь этих четырёх прямоугольников равна \(4ab\), что совпадает с полученным алгебраическим результатом. Таким образом, утверждение доказано и алгебраически, и геометрически.