ГДЗ по Алгебре 7 Класс Номер 739 Дорофеев, Суворова — Подробные Ответы

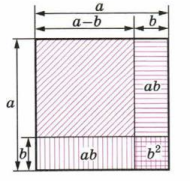
МОДЕЛИРУЕМ Проиллюстрируйте с помощью рисунка 7.7 формулу \((a — b)^2 = a^2 — 2ab + b^2.\)

Пусть \(a^{2}\) — площадь большого квадрата со стороной \(a\).

Площадь меньшего квадрата со стороной \(a — b\) равна \((a — b)^{2}\).

Раскроем скобки:
\((a — b)^{2} = a^{2} — b(a — b) — b(a — b) — b^{2} = a^{2} — ab + b^{2} — ab + b^{2} — b^{2} =\)
\(= a^{2} — 2ab + b^{2}\).

Таким образом, \((a — b)^{2} = a^{2} — 2ab + b^{2}\), что и требовалось доказать.

Рассмотрим квадрат со стороной a, площадь которого равна \(a^{2}\). Внутри этого квадрата выделим меньший квадрат со стороной b, площадь которого равна \(b^{2}\). Тогда сторона оставшейся фигуры равна \(a — b\), и нам нужно найти площадь квадрата с этой стороной, то есть \((a — b)^{2}\).

Для вычисления \((a — b)^{2}\) раскроем скобки по формуле квадрата разности: \((a — b)^{2} = (a — b)(a — b)\). Раскроем произведение: \(a \cdot a — a \cdot b — b \cdot a + b \cdot b\), что даёт \(a^{2} — ab — ab + b^{2}\). Сложим одинаковые слагаемые: \(- ab — ab = — 2ab\). В итоге получаем выражение \(a^{2} — 2ab + b^{2}\).

Таким образом, площадь квадрата со стороной \(a — b\) равна площади большого квадрата \(a^{2}\), минус площадь двух прямоугольников с общей площадью \(2ab\), плюс площадь меньшего квадрата \(b^{2}\). Это и подтверждает формулу \((a — b)^{2} = a^{2} — 2ab + b^{2}\), которая является алгебраическим выражением площади оставшейся части после вычитания меньшего квадрата и двух прямоугольников из большого квадрата.