Учебник «Алгебра. 7 класс» авторов Дорофеев Г.В. и Суворова С.Б. — это современное пособие, которое помогает школьникам сделать первые серьезные шаги в изучении алгебры. Книга рассчитана на широкий круг учеников и отличается продуманной структурой, доступным языком и большим количеством разнообразных задач.
ГДЗ по Алгебре 7 Класс Номер 714 Дорофеев, Суворова — Подробные Ответы
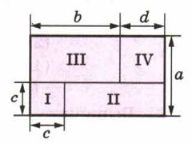
Составьте два выражения для вычисления площади прямоугольника (рис. 7.5) и запишите соответствующее равенство. Докажите это равенство алгебраически.
Площадь I прямоугольника \( S_1 = c \cdot c = c^2 \);
Площадь II прямоугольника \( S_2 = (b + d — c) \cdot c \);
Площадь III прямоугольника \( S_3 = b \cdot (a — c) \);
Площадь IV прямоугольника \( S_4 = d \cdot (a — c) \);
Тогда площадь большого прямоугольника равна:
\( c^2 + (b + d — c) \cdot c + b \cdot (a — c) + d \cdot (a — c) = c^2 + bc + dc — c^2 + ab — ac + ad — dc \).
Упрощаем: \( c^2 + bc + dc — c^2 + ab — ac + ad — dc = ab + ad — ac \).
Или, площадь всего прямоугольника равна: \( (b + d) \cdot a = ab + ad \).
Следовательно:
\( (b + d) \cdot a = c^2 + (b + d — c) \cdot c + b \cdot (a — c) + d \cdot (a — c) \), что и требовалось доказать.
Площадь I прямоугольника: \( S_1 = c \cdot c = c^2 \). Это выражение даёт площадь квадрата, у которого каждая сторона равна \( c \).
Площадь II прямоугольника: \( S_2 = (b + d — c) \cdot c \). Здесь, для прямоугольника с одной стороной длины \( c \), а другой — \( b + d — c \), мы умножаем эти стороны, чтобы получить его площадь.
Площадь III прямоугольника: \( S_3 = b \cdot (a — c) \). В этом случае одна из сторон прямоугольника равна \( b \), а другая — \( a — c \), и площадь вычисляется как произведение этих сторон.
Площадь IV прямоугольника: \( S_4 = d \cdot (a — c) \). Для последнего прямоугольника одна из сторон равна \( d \), а другая — \( a — c \), так что площадь снова вычисляется как произведение сторон.
Теперь, чтобы найти площадь всего большого прямоугольника, сложим площади всех этих частей:
\( S = c^2 + (b + d — c) \cdot c + b \cdot (a — c) + d \cdot (a — c) \).
Раскрываем скобки и упрощаем выражение:
\( c^2 + (b + d — c) \cdot c = c^2 + bc + dc — c^2 \);
\( b \cdot (a — c) = ab — ac \);
\( d \cdot (a — c) = ad — dc \).
Теперь соберём все выражения вместе: \( c^2 + bc + dc — c^2 + ab — ac + ad — dc \). Здесь видно, что \( c^2 \) и \( -c^2 \) взаимно уничтожаются, а \( dc \) и \( -dc \) тоже сокращаются.
Остаток: \( bc + ab — ac + ad \). Мы видим, что остаются только выражения вида \( ab + ad \), что даёт в итоге:
\( ab + ad = (b + d) \cdot a \). Это и есть площадь всего прямоугольника, выраженная через произведение длины стороны \( a \) на сумму \( b + d \).
Итак, получаем следующее равенство: \( (b + d) \cdot a = c^2 + (b + d — c) \cdot c + b \cdot (a — c) + d \cdot (a — c) \), что и требовалось доказать.
