ГДЗ по Алгебре 7 Класс Номер 708 Дорофеев, Суворова — Подробные Ответы

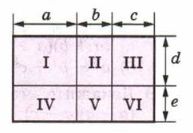
С помощью рисунка 7.4 проиллюстрируйте равенство \((a + b + c)(d + e) = ad + bd + cd + ae + be + ce\).

Докажите это равенство с помощью преобразований.

\(a + b + c)(d + e) = ad + bd + cd + ae + be + ce\).

Чтобы найти площадь большого прямоугольника, нужно сложить площади шести маленьких прямоугольников:

I прямоугольник \(ad\);

II прямоугольник \(bd\);

III прямоугольник \(cd\);

IV прямоугольник \(ae\);

V прямоугольник \(be\);

VI прямоугольник \(ce\);

\(ad + bd + cd + ae + be + ce\).

Или сначала сложить все части длина, затем — все части ширина и перемножить их:

\(a + b + c)(d + e)\).

В итоге, полученные площади будут равны. Следовательно:

\(a + b + c)(d + e) = ad + bd + cd + ae + be + ce\).

\(a + b + c)(d + e) = ad + bd + cd + ae + be + ce\).

Чтобы доказать данное равенство, рассмотрим большой прямоугольник, длина которого состоит из трёх частей: \(a\), \(b\) и \(c\), а ширина состоит из двух частей: \(d\) и \(e\). Таким образом, общая длина прямоугольника равна \(a + b + c\), а общая ширина равна \(d + e\).

Для нахождения площади этого большого прямоугольника можно воспользоваться двумя способами.

Первый способ: Найти площади всех маленьких прямоугольников, из которых состоит большой, и сложить их.

Площадь первого прямоугольника: \(ad\) — произведение длины \(a\) на ширину \(d\).

Площадь второго прямоугольника: \(bd\) — произведение длины \(b\) на ширину \(d\).

Площадь третьего прямоугольника: \(cd\) — произведение длины \(c\) на ширину \(d\).

Площадь четвёртого прямоугольника: \(ae\) — произведение длины \(a\) на ширину \(e\).

Площадь пятого прямоугольника: \(be\) — произведение длины \(b\) на ширину \(e\).

Площадь шестого прямоугольника: \(ce\) — произведение длины \(c\) на ширину \(e\).

Сложив все найденные площади, получаем:

\(ad + bd + cd + ae + be + ce\).

Второй способ: Сначала сложить все части длины: \(a + b + c\), затем сложить все части ширины: \(d + e\), и перемножить полученные суммы:

\(a + b + c)(d + e)\).

По свойству распределительности умножения относительно сложения:

\(a + b + c)(d + e) = a(d + e) + b(d + e) + c(d + e)\).

Раскрывая скобки в каждом слагаемом:

\(= ad + ae + bd + be + cd + ce\).

Переставив слагаемые в удобном порядке, получаем:

\(= ad + bd + cd + ae + be + ce\).

Таким образом, оба способа приводят к одному и тому же результату, что и доказывает данное равенство:

\(a + b + c)(d + e) = ad + bd + cd + ae + be + ce\).