
Учебник «Алгебра. 7 класс» авторов Дорофеев Г.В. и Суворова С.Б. — это современное пособие, которое помогает школьникам сделать первые серьезные шаги в изучении алгебры. Книга рассчитана на широкий круг учеников и отличается продуманной структурой, доступным языком и большим количеством разнообразных задач.
ГДЗ по Алгебре 7 Класс Номер 700 Дорофеев, Суворова — Подробные Ответы
Докажите, что если \( \frac{a}{b} = \frac{c}{d} \), то:
a) \( \frac{a + b}{b} = \frac{c + d}{d} \);
б) \( \frac{a — b}{b} = \frac{c — d}{d} \);
в) \( \frac{a + c}{b + d} = \frac{a}{b} \);
Проиллюстрируйте доказанное утверждение примером.
\( \frac{a}{b} = \frac{c}{d} \) по свойству пропорции: \( ad = bc \);
a) \( \frac{a + b}{b} = \frac{c + d}{d} \);
\( \frac{a + b}{b} = \frac{c + d}{d} \);
\( \frac{a}{b} + 1 = \frac{c}{d} + 1 \);
\( \frac{a}{b} = \frac{c}{d} \);
б) \( \frac{a — b}{b} = \frac{c — d}{d} \);
\( \frac{a}{b} — 1 = \frac{c}{d} — 1 \);
\( \frac{a}{b} = \frac{c}{d} \);
в) \( \frac{a + c}{b + d} = \frac{a}{b} \);
\( b(a + c) = a(b + d) \);
\( ab + bc = ab + ad \);
\( bc = ad \);
\( \frac{a}{b} = \frac{c}{d} \) по свойству пропорции: \( ad = bc \);
a) \( \frac{a + b}{b} = \frac{c + d}{d} \);
Начнем с того, что выражаем каждое из данных выражений в виде дробей:
\( \frac{a + b}{b} = \frac{c + d}{d} \);
Теперь можем разложить дроби на две части:
\( \frac{a}{b} + \frac{b}{b} = \frac{c}{d} + \frac{d}{d} \);
Так как \( \frac{b}{b} = 1 \) и \( \frac{d}{d} = 1 \), мы получаем:
\( \frac{a}{b} + 1 = \frac{c}{d} + 1 \);
Теперь, вычитая 1 с обеих сторон, получаем:
\( \frac{a}{b} = \frac{c}{d} \), что и требовалось доказать, так как мы возвращаемся к первоначальной пропорции.
б) \( \frac{a — b}{b} = \frac{c — d}{d} \);
Рассмотрим выражение:
\( \frac{a — b}{b} = \frac{c — d}{d} \);
Мы можем выделить дроби, как и в предыдущем шаге:
\( \frac{a}{b} — \frac{b}{b} = \frac{c}{d} — \frac{d}{d} \);
Преобразуем выражения, получаем:
\( \frac{a}{b} — 1 = \frac{c}{d} — 1 \);
И снова, вычитая 1 с обеих сторон, мы получаем:
\( \frac{a}{b} = \frac{c}{d} \), что снова подтверждает нашу исходную пропорцию.
в) \( \frac{a + c}{b + d} = \frac{a}{b} \);
Теперь рассмотрим третий случай:
\( \frac{a + c}{b + d} = \frac{a}{b} \);
Для того чтобы доказать это, умножим обе стороны на \( b + d \), чтобы избавиться от знаменателей:
\( b(a + c) = a(b + d) \);
Теперь раскроем скобки с обеих сторон:
\( ab + bc = ab + ad \);
После сокращения термина \( ab \) с обеих сторон, получаем:
\( bc = ad \), что подтверждает равенство, так как оно совпадает с тем, что было дано в начале, и соответствует свойству пропорции.


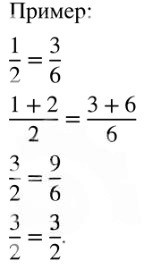
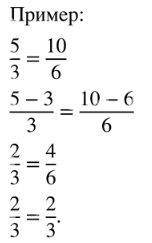
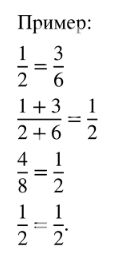
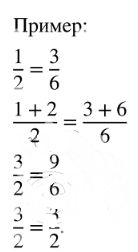


Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!