
Учебник «Алгебра. 7 класс» авторов Дорофеев Г.В. и Суворова С.Б. — это современное пособие, которое помогает школьникам сделать первые серьезные шаги в изучении алгебры. Книга рассчитана на широкий круг учеников и отличается продуманной структурой, доступным языком и большим количеством разнообразных задач.
ГДЗ по Алгебре 7 Класс Номер 685 Дорофеев, Суворова — Подробные Ответы
Иногда удобно вести запись умножения в столбик:
\( -5a^2 \times (3a^3 — a + 4) = -15a^5 + 5a^4 — 20a^2 \).
Умножьте одночлен на многочлен:
а) \( 3n^4(n^2 + 2n — 4) \);
б) \( -2m^3(3m — 2m^2 + m^3) \);
в) \( 5xy^2(2x — x^2y — x^3) \).
а) \( 3n^4(n^2 + 2n — 4) = 3n^6 + 6n^5 — 12n^4 \);
б) \( -2m^3(3m — 2m^2 + m^3) = -6m^4 + 4m^5 — 2m^6 \);
в) \( 5xy^2(2x — x^2y — x^3) = 10x^2y^2 — 5x^3y^3 — 5x^4y^2 \).
а) Рассмотрим выражение \( 3n^4(n^2 + 2n — 4) \). Мы умножаем многочлен \( n^2 + 2n — 4 \) на коэффициент \( 3n^4 \). Раскроем скобки и умножим каждый член на \( 3n^4 \):
\( 3n^4(n^2 + 2n — 4) = 3n^4 \cdot n^2 + 3n^4 \cdot 2n + 3n^4 \cdot (-4) = 3n^6 + 6n^5 — 12n^4 \).
Таким образом, выражение раскрывается в виде:
\( 3n^6 + 6n^5 — 12n^4 \).
б) Теперь рассмотрим выражение \( -2m^3(3m — 2m^2 + m^3) \). Мы умножаем многочлен \( 3m — 2m^2 + m^3 \) на коэффициент \( -2m^3 \). Раскроем скобки и умножим каждый член на \( -2m^3 \):
\( -2m^3(3m — 2m^2 + m^3) = -2m^3 \cdot 3m — 2m^3 \cdot (-2m^2) — 2m^3 \cdot m^3 =\)
\(= -6m^4 + 4m^5 — 2m^6 \).
Таким образом, раскрытое выражение будет:
\( -6m^4 + 4m^5 — 2m^6 \).
в) Рассмотрим выражение \( 5xy^2(2x — x^2y — x^3) \). Мы умножаем многочлен \( 2x — x^2y — x^3 \) на коэффициент \( 5xy^2 \). Раскроем скобки и умножим каждый член на \( 5xy^2 \):
\( 5xy^2(2x — x^2y — x^3) = 5xy^2 \cdot 2x + 5xy^2 \cdot (-x^2y) + 5xy^2 \cdot (-x^3) =\)
\(= 10x^2y^2 — 5x^3y^3 — 5x^4y^2 \).
Таким образом, раскрытое выражение будет:
\( 10x^2y^2 — 5x^3y^3 — 5x^4y^2 \).


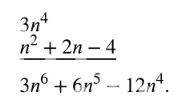
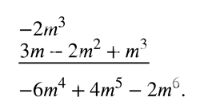
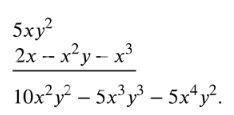


Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!