Учебник «Алгебра. 7 класс» авторов Дорофеев Г.В. и Суворова С.Б. — это современное пособие, которое помогает школьникам сделать первые серьезные шаги в изучении алгебры. Книга рассчитана на широкий круг учеников и отличается продуманной структурой, доступным языком и большим количеством разнообразных задач.
ГДЗ по Алгебре 7 Класс Номер 681 Дорофеев, Суворова — Подробные Ответы
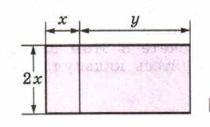
Найдите двумя способами площадь прямоугольника (рис. 7.2) и запишите соответствующее равенство.
Площадь прямоугольника можно найти, если сторону \( 2x \) умножим на сумму сторон \( x + y \), то есть \( 2x(x + y) \).
Или, сначала найдем площадь одного прямоугольника \( 2x \cdot a \), а затем площадь второго прямоугольника \( 2x \cdot y \), и полученные произведения сложим, то есть \( 2x^2 + 2xy \).
Следовательно:
\( 2x(x + y) = 2x^2 + 2xy. \)
Площадь прямоугольника можно найти, если одну из сторон, обозначим её как \( 2x \), умножим на сумму других сторон прямоугольника \( x + y \). В таком случае, по определению площади прямоугольника, мы получаем выражение для площади:
\( 2x(x + y) \),
где \( 2x \) — это одна из сторон, а \( x + y \) — это сумма двух других сторон прямоугольника. Это выражение даёт нам искомую площадь.
Другим способом можно сначала найти площадь одного прямоугольника с длиной стороны \( 2x \) и шириной \( a \), то есть площадь будет равна \( 2x \cdot a \). Затем можно найти площадь второго прямоугольника, где одна из сторон равна \( 2x \), а другая сторона равна \( y \), то есть площадь второго прямоугольника будет \( 2x \cdot y \). После этого полученные площади можно сложить, и получится следующее выражение для общей площади:
\( 2x \cdot a + 2x \cdot y = 2x(a + y) \).
Также, если рассматривать произведения этих выражений, получаем:
\( 2x^2 + 2xy \),
что является результатом сложения произведений \( 2x \cdot a \) и \( 2x \cdot y \).
Следовательно, результат выражается следующим образом:
\( 2x(x + y) = 2x^2 + 2xy. \)
