ГДЗ по Алгебра 7 Класс Номер 68 Дорофеев, Суворова — Подробные Ответы

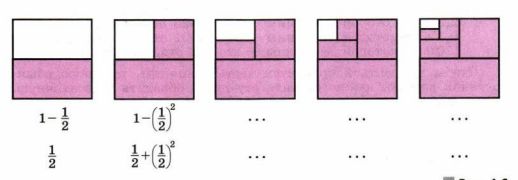
ИССЛЕДУЕМ Квадрат со стороной 1 м закрашивают по час-
тям, как показано на рисунке 1.6. На каждом шаге закрашива-
ется половина незакрашенной части.
1) Для первых двух квадратов записаны по два выражения для
вычисления площади закрашенной части. Запишите соответ-
ствующие выражения для остальных квадратов на рисунке.
2) Запишите два разных выражения для вычисления площади
закрашенной части квадрата, получившейся на десятом шаге;
на сотом шаге.
3) Используйте полученный результат для вычисления значе-
ния выражения
\(\frac{1}{2}+\left(\frac{1}{2}\right)^{2}+\left(\frac{1}{2}\right)^{3}+\ldots+\left(\frac{1}{2}\right)^{10}\).

1) 3 квадрат:

Площадь незакрашенной части после 3-го шага: \(1-\left(\frac{1}{2}\right)^{3}=1-\frac{1}{8}=\frac{7}{8}\).

Площадь закрашенной части после 3-го шага: \(\frac{1}{2}+\left(\frac{1}{2}\right)^{2}+\left(\frac{1}{2}\right)^{3}=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}=\frac{4+2+1}{8}=\frac{7}{8}\).

4 квадрат:

Площадь незакрашенной части: \(1-\left(\frac{1}{2}\right)^{4}=1-\frac{1}{16}=\frac{15}{16}\).

Площадь закрашенной части: \(\frac{1}{2}+\left(\frac{1}{2}\right)^{2}+\left(\frac{1}{2}\right)^{3}+\left(\frac{1}{2}\right)^{4}=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}=\frac{8+4+2+1}{16}=\frac{15}{16}\).

5 квадрат:

Площадь незакрашенной части: \(1-\left(\frac{1}{2}\right)^{5}=1-\frac{1}{32}=\frac{31}{32}\).

Площадь закрашенной части: \(\frac{1}{2}+\left(\frac{1}{2}\right)^{2}+\left(\frac{1}{2}\right)^{3}+\left(\frac{1}{2}\right)^{4}+\left(\frac{1}{2}\right)^{5}=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}=\frac{16+8+4+2+1}{32}=\frac{31}{32}\).

2) 10 шаг:

Площадь незакрашенной части: \(1-\left(\frac{1}{2}\right)^{10}\).

Площадь закрашенной части: \(\frac{1}{2}+\left(\frac{1}{2}\right)^{2}+\left(\frac{1}{2}\right)^{3}+\ldots+\left(\frac{1}{2}\right)^{10}\).

100 шаг:

Площадь незакрашенной части: \(1-\left(\frac{1}{2}\right)^{100}\).

Площадь закрашенной части: \(\frac{1}{2}+\left(\frac{1}{2}\right)^{2}+\left(\frac{1}{2}\right)^{3}+\ldots+\left(\frac{1}{2}\right)^{99}+\left(\frac{1}{2}\right)^{100}\).

3) \(\frac{1}{2}+\left(\frac{1}{2}\right)^{2}+\left(\frac{1}{2}\right)^{3}+\ldots+\left(\frac{1}{2}\right)^{10}=1-\left(\frac{1}{2}\right)^{10}=1-\frac{1}{1024}=\frac{1023}{1024}\).

1) Рассмотрим, как выражаются площади закрашенной и незакрашенной частей квадрата на разных шагах. На каждом шаге закрашивается половина той части квадрата, которая еще остается незакрашенной. Поэтому после первого шага незакрашенной остается половина площади, то есть \(\left(\frac{1}{2}\right)^{1}\), после второго шага незакрашенной останется половина от оставшейся половины, то есть \(\left(\frac{1}{2}\right)^{2}\), после третьего шага \(\left(\frac{1}{2}\right)^{3}\) и так далее. В общем виде после \(n\)-го шага площадь незакрашенной части равна \(\left(\frac{1}{2}\right)^{n}\), а площадь закрашенной части равна \(1-\left(\frac{1}{2}\right)^{n}\), так как весь квадрат имеет площадь 1.

Для 3 квадрата по условию нам нужно записать два выражения: одно через разность \(1-\left(\frac{1}{2}\right)^{3}\) и второе – через сумму всех закрашенных долей по шагам. На 1‑м шаге закрашивается \(\frac{1}{2}\) площади квадрата, на 2‑м шаге закрашивается половина остатка, то есть \(\frac{1}{2}\cdot\frac{1}{2}=\left(\frac{1}{2}\right)^{2}=\frac{1}{4}\), на 3‑м шаге закрашивается половина от оставшейся незакрашенной части, то есть \(\left(\frac{1}{2}\right)^{3}=\frac{1}{8}\). Поэтому площадь закрашенной части после 3 шагов выражается как сумма: \(\frac{1}{2}+\left(\frac{1}{2}\right)^{2}+\left(\frac{1}{2}\right)^{3}=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}\). Приведем к общему знаменателю 8: \(\frac{1}{2}=\frac{4}{8}\), \(\frac{1}{4}=\frac{2}{8}\), \(\frac{1}{8}=\frac{1}{8}\), тогда сумма равна \(\frac{4}{8}+\frac{2}{8}+\frac{1}{8}=\frac{4+2+1}{8}=\frac{7}{8}\). Это совпадает с выражением через разность: \(1-\left(\frac{1}{2}\right)^{3}=1-\frac{1}{8}=\frac{8}{8}-\frac{1}{8}=\frac{7}{8}\).

Для 4 квадрата аналогично: площадь незакрашенной части после 4 шагов равна \(\left(\frac{1}{2}\right)^{4}=\frac{1}{16}\), поэтому площадь закрашенной части через разность равна \(1-\left(\frac{1}{2}\right)^{4}=1-\frac{1}{16}=\frac{16}{16}-\frac{1}{16}=\frac{15}{16}\). Через сумму шагов: на 1‑м шаге \(\frac{1}{2}\), на 2‑м \(\left(\frac{1}{2}\right)^{2}=\frac{1}{4}\), на 3‑м \(\left(\frac{1}{2}\right)^{3}=\frac{1}{8}\), на 4‑м \(\left(\frac{1}{2}\right)^{4}=\frac{1}{16}\). Тогда суммарная закрашенная площадь \(\frac{1}{2}+\left(\frac{1}{2}\right)^{2}+\left(\frac{1}{2}\right)^{3}+\left(\frac{1}{2}\right)^{4}=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}\). Приведем все дроби к знаменателю 16: \(\frac{1}{2}=\frac{8}{16}\), \(\frac{1}{4}=\frac{4}{16}\), \(\frac{1}{8}=\frac{2}{16}\), \(\frac{1}{16}=\frac{1}{16}\). Тогда \(\frac{8}{16}+\frac{4}{16}+\frac{2}{16}+\frac{1}{16}=\frac{8+4+2+1}{16}=\frac{15}{16}\), что совпадает с результатом по формуле \(1-\left(\frac{1}{2}\right)^{4}\).

Для 5 квадрата: незакрашенная часть после 5 шагов \(\left(\frac{1}{2}\right)^{5}=\frac{1}{32}\), закрашенная через разность \(1-\left(\frac{1}{2}\right)^{5}=1-\frac{1}{32}=\frac{32}{32}-\frac{1}{32}=\frac{31}{32}\). По сумме долей: \(\frac{1}{2}+\left(\frac{1}{2}\right)^{2}+\left(\frac{1}{2}\right)^{3}+\left(\frac{1}{2}\right)^{4}+\left(\frac{1}{2}\right)^{5}=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}\). Приводим все дроби к знаменателю 32: \(\frac{1}{2}=\frac{16}{32}\), \(\frac{1}{4}=\frac{8}{32}\), \(\frac{1}{8}=\frac{4}{32}\), \(\frac{1}{16}=\frac{2}{32}\), \(\frac{1}{32}=\frac{1}{32}\). Тогда сумма равна \(\frac{16+8+4+2+1}{32}=\frac{31}{32}\), что снова совпадает с выражением через разность.

2) Теперь запишем два разных выражения для закрашенной части на 10‑м и 100‑м шагах. В общем случае, как уже отмечено, после \(n\)-го шага незакрашенной остается \(\left(\frac{1}{2}\right)^{n}\), поэтому закрашенная часть равна \(1-\left(\frac{1}{2}\right)^{n}\). Это первое, более короткое выражение. Второе выражение – это сумма всех долей, закрашенных на каждом шаге от 1 до \(n\): на 1‑м шаге закрашивается \(\left(\frac{1}{2}\right)^{1}\), на 2‑м \(\left(\frac{1}{2}\right)^{2}\), на 3‑м \(\left(\frac{1}{2}\right)^{3}\), и так далее, до \(\left(\frac{1}{2}\right)^{n}\). То есть закрашенная часть после \(n\)-го шага равна сумме геометрической прогрессии \(\frac{1}{2}+\left(\frac{1}{2}\right)^{2}+\left(\frac{1}{2}\right)^{3}+\ldots+\left(\frac{1}{2}\right)^{n}\).

Для 10 шага первое выражение для площади закрашенной части: \(1-\left(\frac{1}{2}\right)^{10}\). Второе выражение для той же площади: \(\frac{1}{2}+\left(\frac{1}{2}\right)^{2}+\left(\frac{1}{2}\right)^{3}+\ldots+\left(\frac{1}{2}\right)^{10}\). Они равны между собой, так как одно описывает «остаток от целого» (квадрат минус незакрашенная часть), а второе – сумму всех закрашенных шагов отдельно.

Для 100 шага аналогично: первое выражение для закрашенной площади: \(1-\left(\frac{1}{2}\right)^{100}\). Второе выражение через сумму: \(\frac{1}{2}+\left(\frac{1}{2}\right)^{2}+\left(\frac{1}{2}\right)^{3}+\ldots+\left(\frac{1}{2}\right)^{99}+\left(\frac{1}{2}\right)^{100}\). Здесь также эти два выражения описывают одну и ту же величину – площадь закрашенной части квадрата, только представлены в разных формах: компактной (через разность) и развёрнутой (как сумма членов геометрической прогрессии).

3) Для вычисления значения выражения \(\frac{1}{2}+\left(\frac{1}{2}\right)^{2}+\left(\frac{1}{2}\right)^{3}+\ldots+\left(\frac{1}{2}\right)^{10}\) используем связь с площадью квадрата после 10 шагов. Из предыдущего пункта видно, что эта сумма описывает площадь закрашенной части квадрата к 10‑му шагу. Но мы уже знаем, что та же площадь равна \(1-\left(\frac{1}{2}\right)^{10}\). Значит, выражение \(\frac{1}{2}+\left(\frac{1}{2}\right)^{2}+\left(\frac{1}{2}\right)^{3}+\ldots+\left(\frac{1}{2}\right)^{10}=1-\left(\frac{1}{2}\right)^{10}\).

Теперь найдём численное значение \(\left(\frac{1}{2}\right)^{10}\). Так как \(\left(\frac{1}{2}\right)^{10}=\frac{1^{10}}{2^{10}}=\frac{1}{1024}\), то \(1-\left(\frac{1}{2}\right)^{10}=1-\frac{1}{1024}\). Преобразуем: \(1=\frac{1024}{1024}\), тогда \(1-\frac{1}{1024}=\frac{1024}{1024}-\frac{1}{1024}=\frac{1023}{1024}\). Итак, значение выражения \(\frac{1}{2}+\left(\frac{1}{2}\right)^{2}+\left(\frac{1}{2}\right)^{3}+\ldots+\left(\frac{1}{2}\right)^{10}\) равно \(\frac{1023}{1024}\).