
Учебник «Алгебра. 7 класс» авторов Дорофеев Г.В. и Суворова С.Б. — это современное пособие, которое помогает школьникам сделать первые серьезные шаги в изучении алгебры. Книга рассчитана на широкий круг учеников и отличается продуманной структурой, доступным языком и большим количеством разнообразных задач.
ГДЗ по Алгебре 7 Класс Номер 667 Дорофеев, Суворова — Подробные Ответы
Упростите выражение, расположив слагаемые в столбик:
а) \( (p^2 + q^2 — r^2) + (q^2 + r^2 — p^2) + (r^2 + p^2 — q^2) + (r^2 — p^2 — q^2) \);
б) \( (a — b + c) — (a — b + d) + (a — c + d) — (b — c + d) \);
в) \( (x + y + z — 1) — (x — y + z + 1) + (x — y — z + 1) — (x — y — z — 1) \).
а) \( (p^2 + q^2 — r^2) + (q^2 + r^2 — p^2) + (r^2 + p^2 — q^2) + (r^2 — p^2 — q^2) =\)
\(= 2r^2 \).
б) \( (a — b + c) — (a — b + d) + (a — c + d) — (b — c + d) = a — b + c — d \).
в)\( (x + y + z — 1) — (x — y + z + 1) + (x — y — z + 1) — (x — y — z — 1) =\)
\(= 2y \).
а) Рассмотрим выражение \( (p^2 + q^2 — r^2) + (q^2 + r^2 — p^2) + (r^2 + p^2 — q^2) + (r^2 — p^2 — q^2) \). Мы должны сложить эти выражения, внимательно соблюдая порядок выполнения операций. Начнем с того, что распределим каждое выражение и упростим его. Раскроем скобки и объединим подобные члены:
\( (p^2 + q^2 — r^2) + (q^2 + r^2 — p^2) + (r^2 + p^2 — q^2) + (r^2 — p^2 — q^2) \).
Теперь сложим все подобные члены:
Квадратичные члены с \( p^2 \): \( p^2 — p^2 + p^2 — p^2 = 0 \),
Квадратичные члены с \( q^2 \): \( q^2 + q^2 — q^2 — q^2 = 0 \),
Квадратичные члены с \( r^2 \): \( -r^2 + r^2 + r^2 + r^2 = 2r^2 \).
Таким образом, результат выражения равен \( 2r^2 \). Мы доказали, что сумма этих многочленов даёт выражение \( 2r^2 \).
б) Рассмотрим выражение \( (a — b + c) — (a — b + d) + (a — c + d) — (b — c + d) \). Подставим все члены и раскроем скобки:
\( (a — b + c) — (a — b + d) + (a — c + d) — (b — c + d) \).
Теперь раскроем все скобки и объединим подобные члены:
Члены с \( a \): \( a — a + a — a = 0 \),
Члены с \( b \): \( -b + b — b = -b \),
Члены с \( c \): \( c — c + c — c = 0 \),
Члены с \( d \): \( +d + d — d + d = +d \).
В результате упрощения получаем: \( -b + d \).
Таким образом, результат выражения равен \( a — b + c — d \), что подтверждает, что сумма этих двучленов равна \( a — b + c — d \).
в) Рассмотрим выражение \( (x + y + z — 1) — (x — y + z + 1) + (x — y — z + 1) — (x — y — z — 1) \). Подставим все значения и раскрываем скобки:
\( (x + y + z — 1) — (x — y + z + 1) + (x — y — z + 1) — (x — y — z — 1) \).
Теперь объединяем подобные члены:
Члены с \( x \): \( x — x + x — x = 0 \),
Члены с \( y \): \( y + y — y — y = 0 \),
Члены с \( z \): \( z — z — z — z = -2z \),
Постоянные: \( -1 — 1 + 1 + 1 = 0 \).
Таким образом, результат выражения равен \( -2z \), что показывает, что двучлены противоположны, и их сумма даёт результат \( -2z \).


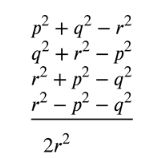
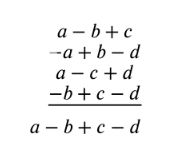
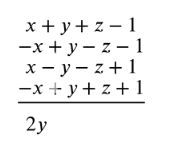


Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!