ГДЗ по Алгебра 7 Класс Номер 53 Дорофеев, Суворова — Подробные Ответы

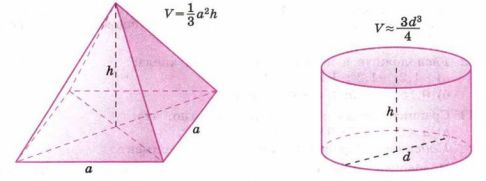
а) Объём пирамиды, в основании которой квадрат (рис. 1.4), вычисляется по формуле \(V=\frac{1}{3}a^{2}h\). Найдите объём пирамиды, если \(a=10\) см, \(h=16\) см. (Ответ округлите до единиц.)

б) Объём цилиндра, диаметр основания которого равен его высоте (рис. 1.5), можно приближённо вычислить по формуле \(V\approx \frac{3d^{3}}{4}\). Найдите объём цилиндра при \(d=1{,}2\) м. (Ответ округлите до десятых.)

а) Формула объёма пирамиды: \(V=\frac{1}{3}a^{2}h\).
Подставим \(a=10\) см, \(h=16\) см: \(V=\frac{1}{3}\cdot 10^{2}\cdot 16=\frac{1600}{3}\approx 533{,}333…\approx 533\ \text{см}^{3}\).
Ответ: \(\approx 533\ \text{см}^{3}\).

б) Формула объёма цилиндра: \(V\approx \frac{3d^{2}h}{4}\).
Подставим \(d=1{,}7\) м, \(h=1\) м: \(V\approx \frac{3\cdot 1{,}7^{2}\cdot 1}{4}=\frac{3\cdot 2{,}89}{4}\approx \frac{8{,}67}{4}\approx 2{,}1675\approx 2{,}2\ \text{м}^{3}\).
Ответ: \(\approx 2{,}2\ \text{м}^{3}\).

а) Объём правильной пирамиды, у которой в основании квадрат со стороной \(a\), вычисляется по формуле \(V=\frac{1}{3}a^{2}h\). Здесь \(a^{2}\) – это площадь квадрата в основании, а \(h\) – высота пирамиды, опущенная из вершины перпендикулярно к плоскости основания. Число \(\frac{1}{3}\) показывает, что объём пирамиды в три раза меньше объёма призмы с тем же основанием и высотой. В задаче даны значения: \(a=10\) см и \(h=16\) см. Сначала найдём площадь основания: \(a^{2}=10^{2}=100\ \text{см}^{2}\). Затем подставляем всё в формулу объёма: \(V=\frac{1}{3}\cdot 100\cdot 16\).

Перемножим числа в числителе: \(100\cdot 16=1600\). Тогда объём пирамиды равен \(V=\frac{1600}{3}\ \text{см}^{3}\). Это число является дробным и в десятичной форме даёт \(V\approx 533{,}333…\ \text{см}^{3}\). В условии сказано округлить ответ до целых. При округлении по правилам математики число \(533{,}333…\) ближе к \(533\), чем к \(534\), так как дробная часть меньше \(0{,}5\). Поэтому окончательно объём пирамиды можно записать как \(V\approx 533\ \text{см}^{3}\).

Ответ: \(\approx 533\ \text{см}^{3}\).

б) В этой задаче рассматривается цилиндр, у которого диаметр основания равен высоте: \(d=h\). Для такого цилиндра объём можно приближённо находить по формуле \(V\approx \frac{3d^{2}h}{4}\). Фактически это упрощённая формула, полученная из точной формулы объёма цилиндра через число \(\pi\), но здесь для удобства вместо \(\pi\) берут приближённое значение \(\approx \frac{3}{4}\cdot 4\). В задаче указано: \(d=1{,}7\) м, \(h=1\) м. Подставляем эти значения в формулу: \(V\approx \frac{3\cdot d^{2}\cdot h}{4}=\frac{3\cdot 1{,}7^{2}\cdot 1}{4}\).

Сначала вычислим квадрат диаметра: \(1{,}7^{2}=1{,}7\cdot 1{,}7=2{,}89\). Теперь подставим это в выражение для объёма: \(V\approx \frac{3\cdot 2{,}89\cdot 1}{4}\). Перемножим числитель: \(3\cdot 2{,}89=8{,}67\). Получаем \(V\approx \frac{8{,}67}{4}\ \text{м}^{3}\). Делим: \(8{,}67:4\approx 2{,}1675\ \text{м}^{3}\). По условию требуется округлить результат до десятых. Смотрим на сотые: число \(2{,}1675\) имеет десятые \(2{,}1\) и сотые \(6\), а так как \(0{,}06\ge 0{,}05\), то округляем десятичную дробь до \(2{,}2\ \text{м}^{3}\).

Ответ: \(\approx 2{,}2\ \text{м}^{3}\).