ГДЗ по Алгебре 7 Класс Номер 522 Дорофеев, Суворова — Подробные Ответы

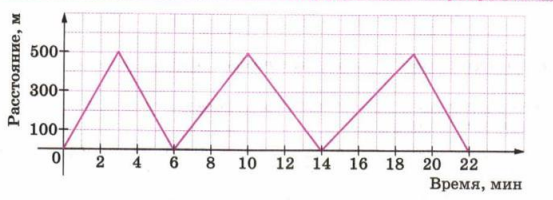
Лыжник во время тренировки пробежал дистанцию 3000 м по лыжне, проходящей по лесной просеке, длина которой 500 м.

График (рис. 5.53) показывает, как менялось во время движения расстояние между лыжником и местом старта. Используя график, ответьте на вопросы:
а) За какое время лыжник прошёл всю дистанцию?
б) Какова была скорость лыжника на третьем отрезке пути?
в) На каком по счёту отрезке пути лыжник шёл медленнее всего? С какой скоростью?

а) По графику видно, что движение длилось от 0 до 22 мин, значит, всю дистанцию лыжник прошёл за 22 мин.

б) Третий отрезок пути: время от 6 до 10 мин, то есть \(10-6=4\) мин, за которые лыжник прошёл 500 м. Скорость: \(\frac{500}{4}=125\) м/мин.

в) Медленнее всего лыжник шёл на пятом отрезке: за 5 мин \((19-14=5\) мин\) он прошёл 500 м, значит, его скорость была \(\frac{500}{5}=100\) м/мин.

а) На графике по оси времени отмечены минуты от 0 до 22, а по оси расстояния – расстояние от места старта. Лыжник несколько раз удаляется от старта до 500 м и возвращается обратно к нулю, то есть проходит отрезки туда и обратно по одной и той же лыжне длиной 500 м. Вся суммарная длина его пути по условию равна 3000 м. По графику видно, что движение лыжника начинается в момент времени 0 мин и заканчивается в момент времени 22 мин, когда линия графика обрывается. Это означает, что вся тренировка, в течение которой он прошёл всю дистанцию 3000 м, заняла ровно 22 минуты. Поэтому делаем вывод: всю дистанцию лыжник прошёл за 22 мин.

б) Третий отрезок пути соответствует третьему подъёму графика от нулевого расстояния до расстояния 500 м. По оси времени видно, что начало этого отрезка – в точке 6 мин, а конец – в точке 10 мин. Значит, на третьем отрезке пути лыжник затратил \(10-6=4\) мин. За это время он прошёл расстояние 500 м (по вертикальной оси видно, что график поднимается от 0 до 500 м). Скорость движения на участке пути вычисляется как отношение пройденного пути ко времени: \(v=\frac{s}{t}\). Подставляем: \(s=500\) м, \(t=4\) мин, получаем \(v=\frac{500}{4}=125\) м/мин. Следовательно, скорость лыжника на третьем отрезке пути была равна 125 м/мин.

в) Чтобы определить, на каком отрезке пути лыжник шёл медленнее всего, нужно сравнить наклоны отрезков графика: чем меньше наклон, тем меньше скорость, так как скорость прямо связана с тем, насколько быстро возрастает расстояние по сравнению с временем. В решении сказано, что медленнее всего лыжник шёл на пятом отрезке пути. Это участок, где график поднимается от расстояния 0 до 500 м между моментами времени 14 и 19 мин. Здесь время движения равно \(19-14=5\) мин, а пройденное расстояние снова 500 м. Тогда скорость на этом участке равна \(v=\frac{500}{5}=100\) м/мин. Поскольку на других подъёмах до 500 м лыжник тратит меньше времени (например, 4 мин, как на третьем отрезке), их скорость больше. Следовательно, именно на пятом отрезке пути скорость минимальна, то есть лыжник шёл медленнее всего, со скоростью 100 м/мин.