ГДЗ по Алгебре 7 Класс Номер 519 Дорофеев, Суворова — Подробные Ответы

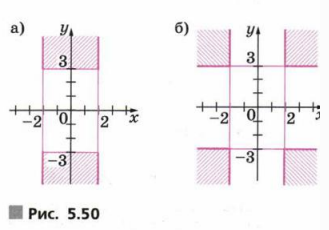
Опишите на алгебраическом языке множества точек координатной плоскости, изображённые на рисунке 5.50, а, б.

a) Множество точек задаётся системой неравенств: \(|y|\ge3\) и \(|x|\le2\). Значит, это все точки, которые лежат вне полосы между прямыми \(y=3\) и \(y=-3\), но при этом их абсциссы находятся в пределах от \(-2\) до \(2\).

б) Множество точек задаётся системой неравенств: \(|y|\ge3\) и \(|x|\ge2\). Это все точки, лежащие вне полосы между прямыми \(y=3\) и \(y=-3\) и одновременно вне вертикальной полосы между прямыми \(x=2\) и \(x=-2\).

a) В условии пункта а) заданы два неравенства: \(|y|\ge3\) и \(|x|\le2\). Неравенство \(|y|\ge3\) означает, что расстояние точки по вертикали от оси \(Ox\) не меньше 3 единиц. Это эквивалентно двойному неравенству \(y\ge3\) или \(y\le-3\). То есть допустимы все точки, лежащие на прямых \(y=3\), \(y=-3\) и вне полосы между ними, выше прямой \(y=3\) и ниже прямой \(y=-3\).

Второе неравенство \(|x|\le2\) ограничивает координату \(x\): расстояние от точки до оси \(Oy\) по горизонтали не больше 2. Это равносильно двойному неравенству \(-2\le x\le2\). Значит, все допустимые точки не выходят за вертикальные прямые \(x=-2\) и \(x=2\), то есть лежат внутри вертикальной полосы, включая её границы.

Совместное выполнение условий \(|y|\ge3\) и \(|x|\le2\) задаёт пересечение этих двух полос: берем только те точки, которые одновременно находятся в вертикальной полосе \(-2\le x\le2\) и вне горизонтальной полосы \(-3<y<3\). Геометрически это две «вертикальные» области над прямой \(y=3\) и под прямой \(y=-3\), но при этом сжаты по горизонтали в промежутке от \(-2\) до \(2\), включая линии \(x=-2\), \(x=2\), \(y=3\) и \(y=-3\).

б) В пункте б) снова присутствует условие \(|y|\ge3\), то есть по вертикали множество точек такое же, как и в пункте а): \(y\ge3\) или \(y\le-3\). Это все точки, которые лежат на прямых \(y=3\), \(y=-3\) и вне промежутка между ними, то есть достаточно далеко от оси абсцисс, на расстоянии не менее 3 единиц.

Однако горизонтальное условие теперь другое: \(|x|\ge2\). Это означает, что расстояние точки от оси \(Oy\) не меньше 2. В алгебраическом виде это записывается как \(x\ge2\) или \(x\le-2\). Таким образом, мы исключаем все точки, у которых абсцисса по модулю меньше 2, то есть все точки внутри вертикальной полосы \(-2<x<2\), а оставляем только те, что находятся на прямых \(x=2\), \(x=-2\) и дальше от них.

При одновременном выполнении \(|y|\ge3\) и \(|x|\ge2\) множества точек образуют пересечение двух «внешних» областей: точки должны быть и достаточно далеко от оси \(Ox\) (по вертикали), и достаточно далеко от оси \(Oy\) (по горизонтали). В результате получаются четыре угловые области (в каждом квадранте координатной плоскости), ограниченные линиями \(y=3\), \(y=-3\), \(x=2\), \(x=-2\), включая сами эти прямые. То есть множество состоит из всех точек, для которых одновременно выполняются условия \(y\ge3\) или \(y\le-3\) и \(x\ge2\) или \(x\le-2\).